Calcul direct du potentiel et du champ électrostatique crées par une distribution continue de charges - Exercices corrigés d'életrostatique
Exercice 1 - Segment de droite uniformément chargé avec la densité linéique
Soit un segment AB uniformément chargé avec une densité linéique λ > 0 (figure 1)On désigne par O le milieu du segment AB. Calculer le champ
crée par cette distribution en tout point M sur une distance a de la médiatrice de AB et en un point M appartenant au segment AB.
Exercice 2- Répartition linéique de charges non uniforme
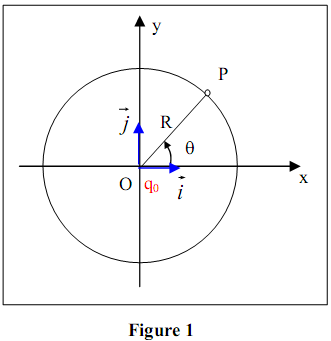
Un fil de section négligeable en forme d’un cercle de centre O et de rayon R placé dans le plan xOy, porte une charge électrique répartie avec une densité linéique λ :
où λ0 est une constante positive et
, P étant un point quelconque du cercle (figure 4). 
Calculons les composantes de la force
exercée sur une charge ponctuelle q0 (>0), placée en O, par l’ensemble de la charge portée par le cercle.
exercée sur une charge ponctuelle q0 (>0), placée en O, par l’ensemble de la charge portée par le cercle. Exercice 3 - Boucle circulaire portant une charge linéique uniforme
Soit une boucle circulaire de centre O, de rayon R, uniformément chargée avec une densité linéique λ0=λ (figure 1). Calculer le champcrée par cette distribution de charges, en un point M de l’axe
de la boucle : a) A partir du potentiel électrostatique
b) Directement
Exercice 4- Boucle circulaire portant une chargée non uniforme
On considère à nouveau la boucle circulaire de centre O, de rayon R, cette fois chargée avec une densité linéique de charge 
, figure 7.
Déterminer le potentiel et le champ électrostatique crées par cette répartition de charges en tout point M de l’axe de la boucle.
, figure 7. Déterminer le potentiel et le champ électrostatique crées par cette répartition de charges en tout point M de l’axe de la boucle.
Exercice 5 - Disque uniformément chargé avec la densité superficielle uniforme
Soit un disque de centre O, de rayon R, uniformément chargé avec une densité surfacique de charge σ > 0 (figure 12). Calculer le champ créé par cette distribution de charges en un point M de l’axe du disque : a) A partir du potentiel électrostatique
b) directement
Exercice 6- Cylindre uniformément chargé en surface latérale avec une densité superficielle uniforme
Considérons un cylindre d’axe z’z et tel que l’origine O soit confondu avec son centre (figure 15). Ce cylindre est uniformément chargé sur sa surface latérale avec une densité superficielle uniforme σ > 0. Calculer le champ électrostatique en un point M de l’axe du cylindre.
∎ Voir la solution
Exercice 7 - Sphère uniformément chargée en surface
Considérons une sphère de centre O, de rayon R et uniformément chargée en surface avec la densité superficielle σ (σ > 0). Choisissons le système d’axes (Oxyz) tel que l’axe Oz soit confondu avec (OM) (figure 17). Calculer le champ électrostatique en un point M de l’axe Oz.
Exercice 8- Calotte sphérique chargée uniformément en surface
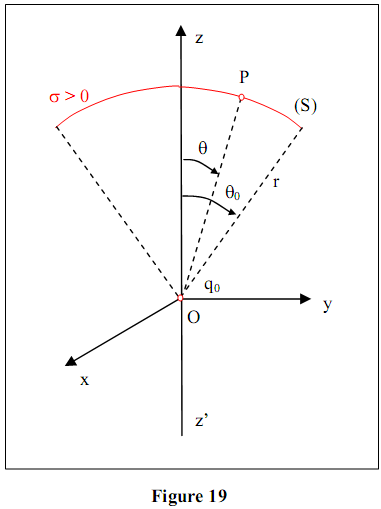
On considère la surface (S) découpée sur une sphère de centre O et de rayon r par un cône de sommet O et de demi-angle au sommet θ0 (calotte sphérique). Cette surface est uniformément chargée avec la densité surfacique σ > 0(figure 19).
qu’elle exerce sur une charge ponctuelle q0 positive placée en O. Exercice 9- Répartition volumique de charges comprise entre deux calottes sphériques
Un cône découpe sur deux sphères, de même centre O et de rayon R1 et R2 (R1 < R2), deux calottes (S1) et (S2). Le volume délimité par (S1) et (S2) et le cône est uniformément chargé avec la densité volumique ρ positive (figure 22).
qu’elle exerce sur une charge ponctuelle q0 positive placée en O.
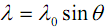
Commentaires
Enregistrer un commentaire