COURS DE LA RECHERCHE OPÉRATIONNELLE

Cours Recherche Opérationnelle

Chapitre 1 : Formulation d’un programme linéaire (PL)
I. Introduction
II. Les conditions de formulation d’un PL
III. Les étapes de formulation d’un PL
IV. Présentation Théorique
V. Exemples de formulations

Chapitre 2 : Résolution d’un programme linéaire (PL)
I. Introduction
II. Système d’axes
III. Représentation graphique des contraintes
IV. Représentation de la fonction objectif
V. Recherche de la solution optimale
a. Résolution graphique
b. Résolution par énumération :
VI. Exemples
VII. Analyse de sensibilité

Chapitre 3 :La Méthode de Simplexe
I. Introduction
II. Mise sous forme standard
III. Revue algébrique de la méthode du simplexe
IV. La méthode des tableaux
a. Tableau de simplexe initial
b. Amélioration de la solution
c. Calcul des tableaux suivants
V. Résumé de la procédure de la méthode du simplexe
VI. Exemple

Chapitre 4 : Problèmes de Minimisation et Problèmes Irréguliers
I. Introduction
II. Les variables artificielles
III. Les problèmes de minimisation
IV. Les problèmes irréguliers
a. Les problèmes impossibles
b. Les problèmes à solutions multiples
c. Les problèmes à solution infinie
d. Les problèmes à solution dégénérée

Chapitre 5 : Dualité et analyse de sensibilité
I. Introduction
II. Interprétation économique
III. Dualité
a. Définition
b. Propriétés et signification économique du programme dual
c. Tableau de correspondance primal-dual
III. Analyse de sensibilité
a. Analyse de sensibilité sur les Cj
b. Analyse de sensibilité sur les bj
c. Analyse de sensibilité sur les coefficients aij
IV. Introduction d’une nouvelle activité
a. Introduction d’une nouvelle variable de décision
b. Introduction d’une nouvelle contrainte

Chapitre 6 : Introduction à la Programmation Dynamique
I. Introduction
II. Exemple prototype. Le problème du voyageur
III. Caractéristiques d’un problème de programmation dynamique
IV. Programmation dynamique déterministe
a. Introduction
b. Problème du type plus court chemin
c. Répartition optimale des moyens
d. Résolution d'un programme linéaire

CHAPITRE 5

Dualité et analyse de sensibilité

I. Introduction

Dans ce chapitre, on va étudier des notions relatives au programmes linéaires tels que le programme dual, les coûts marginaux ainsi que des techniques de validation de la solution d’un programme linéaire, c’est à dire l’analyse de sensibilité.

Nous allons commencer ce chapitre par donner quelques termes clés du jargon utilisé pour interpréter économiquement les différents résultats du programme linéaire.

II. Interprétation économique

Les éléments clés d’un programme linéaire standard sont :

- La fonction objectif dite fonction économique. Cette fonction peut représenter un coût, un profit, etc...

- Les contraintes sont composées, des coefficients aij de la matrice A, dite matrice technologique, et des constantes bi, qui forment le vecteur du second membre. Le second membre peut représenter la disponibilité des ressources, les niveaux de demande etc...

- Les variables d’écart peuvent représenter, par exemple dans le problème de l’agriculteur, l’excédent de chacune des ressources : terrain, eau, heures de travail, bureau d’irrigation. Elles sont aussi dites variables de surplus.

Quand une variable d’écart est nulle, on dit que la contrainte correspondante est saturée. Dans le problème de l’agriculteur les contraintes terrain et main d’œuvre sont saturées. Elles sont dites aussi restrictives car une variation du second membre (par exemple) engendre un changement dans la valeurs de la solution optimale.

Toute contrainte non saturée à l’optimum n’est pas restrictive pour le problème, c’est à dire qu’elle n’a aucune influence sur la solution considérée.

Définition: Coût marginal

Par définition, on appelle coût marginal d’un bien l’augmentation minimale de dépenses, par rapport à la solution optimale, qui résulterait de l’utilisation d’une unité supplémentaire de ce bien, lorsque le problème posé consiste à produire des biens au moindre coût.

Si le problème posé consiste à transformer des biens pour vendre une production avec un meilleur profit et l’augmentation maximale de revenu qui résulte de la possibilité de disposer d’une unité supplémentaire de l’un des biens, est la valeur marginale de ce bien. Très souvent, on emploie également dans ce cas le qualificatif coût marginal.

Remarque : Les coûts marginaux sont donc les effets nets associés aux variables d’écart, puisque ce sont ces variables qui déterminent les excédents (ou les insuffisances) de biens.

Si une variable d’écart n’est pas nulle, dans la solution optimale, c’est que le bien correspondant est déjà excédentaire. Par conséquent, le fait de disposer d’une unité supplémentaire de ce bien n’aura aucune influence sur le revenu. On dit alors que ce bien à une valeur marginale nulle, ou par extension, que la variable d’écart associée à ce bien a une valeur marginale nulle.

Par contre, si une variable d’écart est nulle dans la solution optimale, c’est que le bien correspondant est totalement utilisé. Par la suite une variation de la disponibilité aura généralement une influence sur le revenu. C’est pourquoi cette variable d’écart nulle dans la solution optimale à une valeur marginale non nulle, et cette valeur marginale précise la variation de la fonction économique résultant de l’utilisation d’une unité supplémentaire du bien associé.

Exemple : Dans le problème de l’agriculteur on a

Le coût marginal lié à est

Une augmentation de

d’une unité entraîne une diminution de

de la valeur de la fonction économique.

Le coût marginal lié à est 0 et à l'optimum =0

on a déjà

d’eau de plus donc si on ajoute

ca ne va pas changer la solution optimale ni la valeur de la fonction économique

Le système de contraintes dans le programme linéaire relatif au tableau de simplexe optimal du problème de l’agriculteur est

La fonction économique s’écrit

Si on exprime

en fonction de

(variables hors base) en utilisant le système d’équation ci dessus on a

La valeur 26000 correspond à la valeur optimale de la fonction économique.

alors un hectare de terrain de moins à utiliser, donc une réduction de

dinars de la valeur de la fonction objectif.

Si on ajoute 3 hectares de terrains

, avec l’hypothèse que les autres quantités restent inchangées alors le revenu augmente de

On vérifie ceci, si on résout le programme linéaire

On trouve que la valeur optimale va augmenter de 200 dinars est devient 26 200 dinars.

Exercice : Expliquer graphiquement que si on ajoute des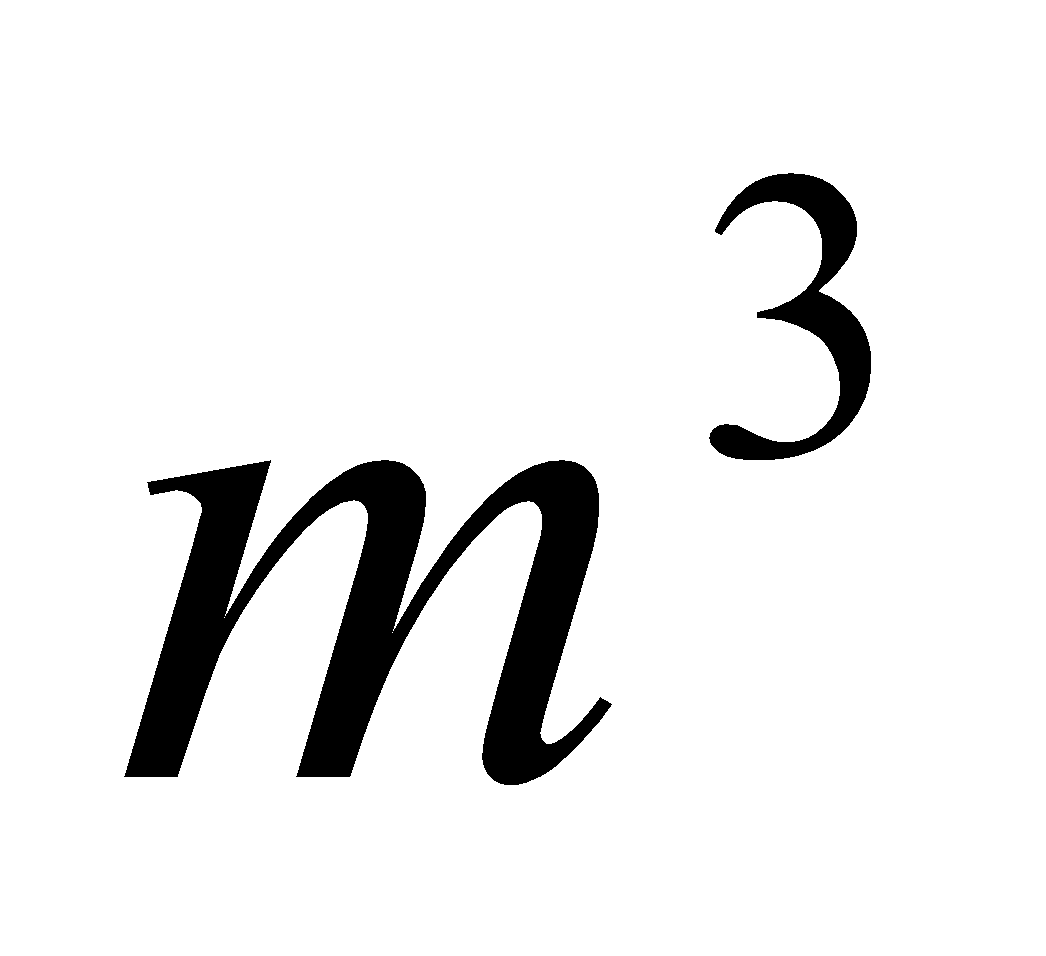

d’eau, on aura aucune amplification dans la fonction objectif.

Remarque : Dans le cas où on diminuerait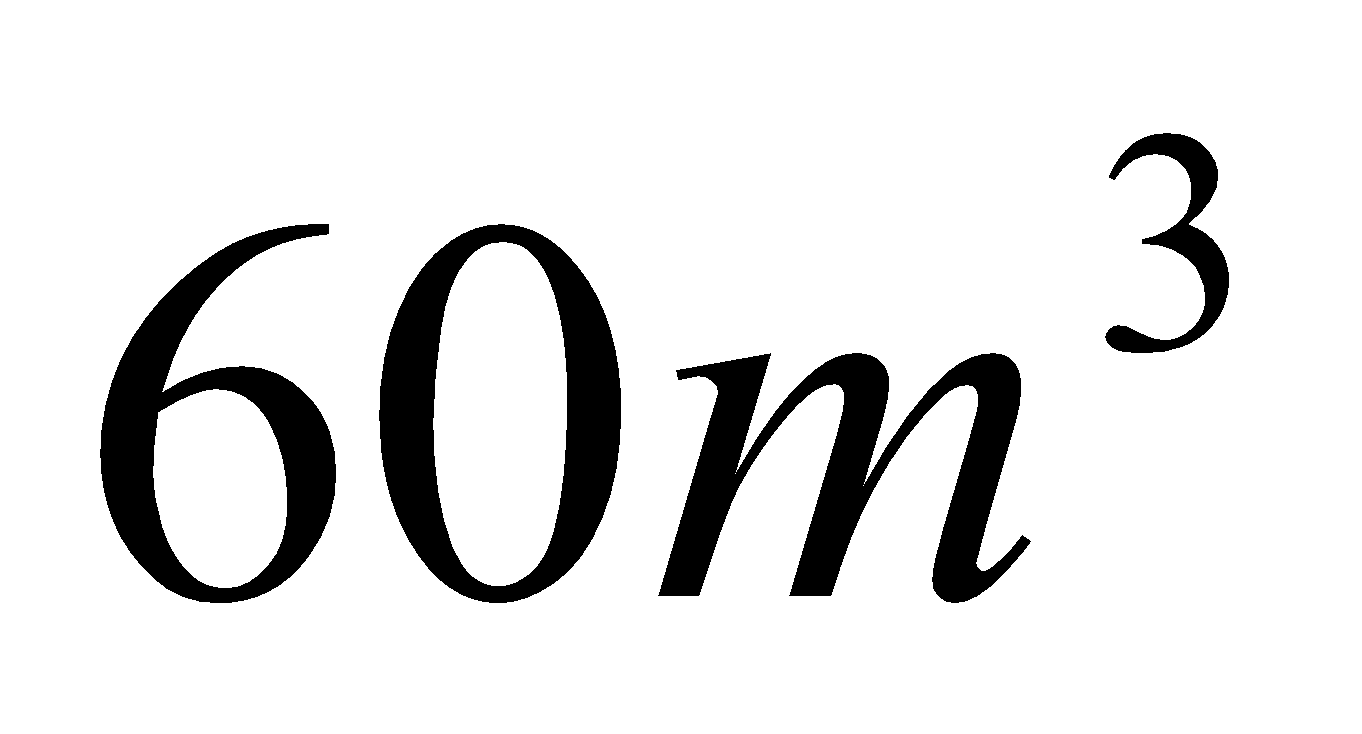

d’eau, la solution optimal devient dégénérée.

Les valeurs marginales apportent donc des renseignements économiques particulièrement intéressantes, mais il faut les utiliser avec prudence car leur domaine de validité est limité.

Par exemple, si on ajoute 30 hectares de terrains aux 150 déjà disponibles dans le problème de l’agriculteur, le revenu augmentera de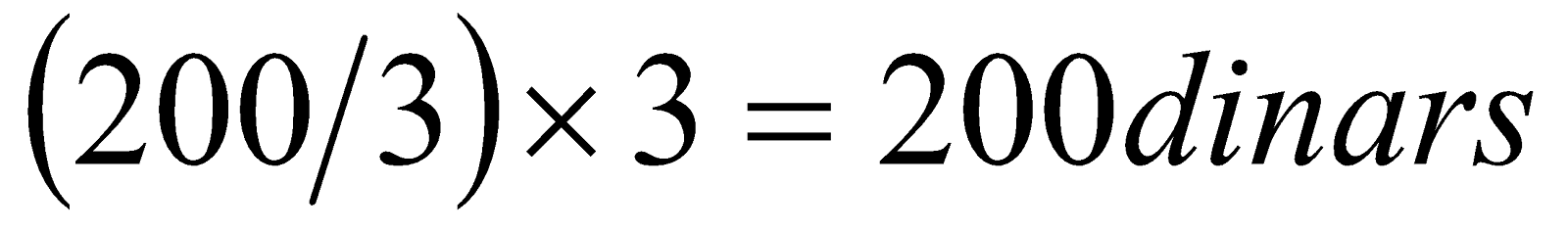

. Ceci n’est pas vrai, parce que si on résout le programme linéaire suivant :

La valeur optimale du programme linéaire ci-dessus est de 26 875,14 donc le revenu n’a pas augmenté de 2000 dinars comme prévu.

III. Dualité

a. Définition

La forme d’un programme linéaire de type maximisation est

avec

des vecteurs de dimensions respectives

, et A une matrice de dimension

On appelle programme dual de

, le programme linéaire suivant :

avec

un vecteur de dimension

la transposée de la matrice

Le programme

est appelé programme Primal.

Pour passer du primal au dual, on remarque que :

Les termes du second membre deviennent les coefficients de la fonction objectif et réciproquement.
Le problème de maximisation devient un problème de minimisation.
Les inégalités deviennent des inégalités
La matrice A se transforme en sa transposée.

Exemple : Le programme primal (problème de l’agriculteur) est

Donc le programme dual est

b. Propriétés et signification économique du programme dual

Pour expliquer la signification du problème dual on va se baser sur l’exemple de l’agriculteur.

Supposons qu’un agriculteur (client) voudrait acheter la totalité de nos ressources disponibles. Notre agriculteur acceptera certainement cette proposition si le prix offert par ce client lui procure le même profit.

soit

le prix d'un hectare de terrain

le prix d’un

d’eau

le prix d’une heure de main d’œuvre

le prix de la permission de la culture d’un hectare de tomates.

Le problème du client consiste à minimiser les frais d’achat des ressources : c’est à dire

sous la contrainte que les prix satisfont notre agriculteur.

Pour notre agriculteur un hectare de terrain

d’eau, une heure de travail et un hectare de permission du bureau est équivalent a un revenu de 100 dinars.

Tandis que, un hectare de terrain,

d’eau et 4 heures de travail lui engendrent un revenu de 200 dinars.

Il n’est prêt à vendre ses ressources que si

lui rapporte un revenu supérieur ou égale à 100 DT et que si

lui rapporte un revenu supérieur ou égal à 200 DT.

Ainsi le problème du client est

Donc le problème du client peut être modélisé par le programme dual.

Le tableau de simplexe final du programme dual est :

			150	440	480	90	0	0
			y1	y2	y3	y4	L1	L2
480	y3	100/3	0	-2/3	1	-1/3	1/3	1/3
150	y1	200/3	1	14/3	0	4/3	-4/3	1/3
			150	380	480	40	-40	-110
			0	60	0	50	40	110

Avec L1 et L2, les variables d’écart à la 1ère et la 2ème contrainte du programme dual.

On remarque que la solution optimale du dual peut être déduite du primal de la manière suivante :

y1 = 200/3 ↔ C3 - z3 = - 200/3

y2 = 0 ↔ C2 - z4 = 0

y3 = 100/3 ↔ C5 - z5 = - 100/3

y4 = 0 ↔ C6 - z6 = 0

L1 = 0 ↔ C1 - z1 = 0

L2 = 0 ↔ C2 - z2 = 0

C1 - z1 = 0 ↔ S1 = 0

C2- z2 = 60 ↔ S2 = 60

C3- z3 = 0 ↔ S3 = 0

C4 - z4= 50 ↔ S4 = 50

C5 - z5= 40 ↔ x1 = 40

C6 - z6= 110 ↔ x2 = 110

w = 26000 ↔ z = 260000

On peut généraliser ce résultat dans le tableau suivant :

Primal (Max)	Dual (Min)
Variables de décision xj = 0 ⇒ Cj - zj < 0 xj > 0 ⇒ Cj - zj = 0	variables d’écart Li = \| Cj - zj \| ≠ 0 ⇒ Cj - zj = 0 Li = 0 ⇒ Cj - zj = xj
variables d’écart Sj = 0 ⇒ Cj - zj ≠ 0 Sj > 0 ⇒ Cj - zj = 0	Variables de décision yi = \| Ci - zj \| ≠ 0 ⇒ Cj - zj = 0 yi = 0 et Cj – zj = Sj

On remarque aussi qu’à l’optimum la valeur de la fonction objectif du dual est égale à la valeur de la fonction objectif du primal.

Proposition : Le dual du programme dual est le programme primal.

c. Tableau de correspondance primal-dual

Max	Min
Matrice des contraintes (m, n) - Second membre des contraintes - Coefficient de la fonction objectif	- Transposée de la matrice des contraintes (n, m) - Coefficient de la fonction objectif - Second membre des contraintes
Nombre de contraintes i ème contrainte de type « ≤ » i ème contrainte de type « ≥ » i ème contrainte de type « = »	Nombre de variables principales i ème variable de type « ≥ 0 » i ème variable de type « ≤ 0 » i ème variable qcq « ∈IR »
Nombre de variables j ème variable « ≥ » j ème variable « ≤ » j ème variable qcq « ∈IR »	Nombre de contraintes j ème contrainte de type « ≥ » j ème contrainte de type « ≤ » i ème contrainte de type « = »

Exemples

Primal	Dual
Max ½ x1 + x2 S.c x1 + x2 ≤ 3 - x1 + x2 ≤ 1 x1 ≤ 2 x1 ≥ 0, x2 ≥ 0	Min 3y1 + y2 + 2y3 S.c y1 - y2 + y3 ≥ ½ y1 + y2 ≥ 1 y1 ≥ 0, y2 ≥ 0, y3 ≥ 0
Min - x1 + x2 S.c 2x1 - x2 ≥ 2 - x1 + 2x2 ≥ -2 x1 + x2 ≤ 5 x1 ≥ 0, x2 ≥ 0	Max 2y1 - 2y2 + 5y3 S.c 2y1 - y2 + y3 ≤ -1 - y1 + 2y2 + y3 ≤ 1 y1 ≥ 0, y2 ≥ 0, y3 ≤ 0
Max 2x1 - x2 S.c x1 - x2 = 3 x1 ≤ 4 x1 ≥ 0, x2 ≥ 0	Min 3 y1+ 4 y2 S.c y1+ 2 y2 ≥ 2 - y1 ≥ -1 y1∈IR, y2 ≥ 0
Max 2x1 - x2 S.c x1 - 2x2 ≤ 2 x1 + x2 = 6 x2 ≤ 5 x1∈IR, x2∈IR	Min - 2y1 + 6y2 - 5y3 S.c y1 + y2 = 2 - 2y1 + y2+ y3 = -1 y1 ≥ 0, y2 ∈IR, y3 ≥ 0

IV. Analyse de sensibilité

Définition: Une solution de base optimale est dite stable si l’ensemble des variables de base à l’optimum ne changent pas, même si les valeurs de ces variables de base sont modifiées.

Dans cette section on examinera la stabilité de la solution optimale d’un programme linéaire suite à la variation de l’un des paramètres de ce programme.

On utilisera pour présenter l’analyse de sensibilité sur ces différents paramètres du programme linéaire l’exemple de l’agriculteur.

Max 100x1 + 200x2

S.c x1 + x2 ≤ 150

4x1 + 2x2 ≤ 440

- x1 + 4x2 ≤ 480

x1 ≤ 90

x1 ≥ 0 , x2 ≥ 0

a. Analyse de sensibilité sur les Cj

On cherche à déterminer un intervalle dans lequel peut varier Cj sans que la solution optimale ne change.

Considérons une variation du coefficient Cj de 100 à 100 + Δ

En remplaçant dans le tableau optimal 100 par 100 + Δ , on obtient le tableau suivant :

			100+Δ	200	0	0	0	0
			x1	x2	S1	S2	S3	S4
100+Δ	x1	40	1	0	4/3	0	-1/3	0
0	S2	60	0	0	-14/3	1	2/3	0
200	x2	110	0	1	-1/3	0	1/3	0
0	S4	50	0	0	-4/3	0	1/3	1
			100+Δ	200	(200+4Δ)/3	0	(100-Δ)/3	0
			0	0	-(200+4Δ)/3	0	Δ-100/3	0

La solution donnée par le tableau reste optimale si

Donc la solution optimale est stable et prend la même valeur (x1,x2)=(40,110) tant que 50 ≤ C1 ≤ 200

Exercice : Supposons que le coefficient Cj d'une variable hors base dans la solution optimale, est modifié. Dans quel intervalle, Cj peut-il varier sans que la base optimale soit modifiée ?

(Aide : différencier le cas d’un programme de maximisation et le cas d’un programme de minimisation).

Solution :

- ∞ < Cj ≤ zj cas d’un programme de maximisation

zj ≤ Cj < - ∞ cas d’un programme de minimisation

b. Analyse de sensibilité sur les bj

Déterminer l’intervalle pour lequel, la solution optimale reste stable, pour une variation du second membre de la ième contrainte bi .

Considérons une variation de b1 de 150 à 150 + Δ.

Sachant que dans le premier tableau de simplexe b1 n’est présent que dans la première contrainte. On obtient ainsi une correspondance entre la colonne des quantités Qi et la colonne de S1.

			100	200	0	0	0	0
			x1	x2	S1	S2	S3	S4
0	S1	150+1× Δ	1	1	1	0	0	0
0	S2	440+0× Δ	4	2	0	1	0	0
0	S2	480+0× Δ	1	4	0	0	1	0
0	S4	90+0× Δ	1	0	0	0	0	1
		0+1× Δ	0	0	0	0	0	0
			100	100	0	0	0	0

Dans le tableau optimal, la colonne correspondant à S1 nous donne les coefficients de Δ dans la colonne des quantités.

			100	200	0	0	0	0
			x1	x2	S1	S2	S3	S4
100	x1	40+4/3Δ	1	0	4/3	0	-1/3	0
0	S2	60-14/3Δ	0	0	-14/3	1	2/3	0
200	x2	110-1/3Δ	0	1	-1/3	0	1/3	0
0	S4	50-4/3Δ	0	0	-4/3	0	1/3	1
		26000+200Δ/3	100	200	200/3	0	100/3	0
			0	0	-200/3	0	-100/3	0

La base reste optimale tant que :

⇔ - 30 ≤ Δ ≤ 90/7

Donc tant que 120 ≤ b1 ≤ 160,85 la base demeure la même et la solution optimale est stable mais elle change en valeur (exemple: pour Δ= 3 le vecteur de solutions optimale est (x1,x2,S1,S2,S3,S4)=(44,109,0,46,0,46))

Remarque : D’après le résultat ci-dessus on peut conclure que le coût marginal de 200/3 par hectare de la première ressource n’est valide que si la solution de base demeure stable. Donc si et seulement si 120 ≤ b1 ≤ 160,85. Ceci est appelé le domaine de validité du coût marginal.

Exercice 1:

Sans faire de calcul, de combien peut-on modifier la quantité de m3 d’eau sans nuire à la solution optimale ? confirmez votre résultat a l'aide de la méthode d'analyse de sensibilité exposé ci-dessus ?

Exercice 2 :

Déterminer l’intervalle dans lequel peut varier b1 et b3 (les ressources en surface et en main d’œuvre) sans que la base optimale change.

Réponse 2 :

Pour Δ1 = 0 (variation nulle de la surface en hectare), la solution optimale est stable pour une variation Δ2 des ressources en main d’œuvre entre 570 et 730 heures (-150 ≤ Δ2 ≤ 90).

Le coût marginal de 100/3 par heure de main d’œuvre de la 3ème ressource n’est valide que dans l’intervalle [570, 730].

c. Analyse de sensibilité sur les coefficients aij

Supposons que dans le problème de l’agriculteur, le nombre d’unités de la ième ressources nécessaire pour produire une unité de produit j, soit (aij + δ) ou lieu de aij. Ainsi, on se pose la question si la solution optimale demeure stable suite à un tel changement.

i) xj est une variable de base et la ième ressource est totalement utilisée.

Par exemple : x1 + (4+δ)x2 ≤ 480 ⇒ x1 + (4 + δ )x2 + S3 = 480

A l’optimum, la base est inchangée donc

Si δ ≥ 0 , alors l’équation ne peut pas être satisfaite sinon puisque et .

Si δ ≤ 0 , alors on a un excèdent de la 3ème ressource (S3 ≠ 0), ce qui nous contraint à changer la base (la solution optimale n’est plus stable).

Conclusion: Dans le cas où xj est une variable de base optimale et la ième ressource est totalement utilisée, il est impossible de modifier le coefficient aij sans que la base dans la solution optimale ne change pas (la solution optimale n'est pas satable).

ii) xj est une variable de base et la ième ressource n’est pas totalement utilisée.

Par exemple : (4 +δ) x1 + 2x2 ≤ 440

⇒ (4 + δ )x1 +2x2 + S2 = 440

A l’optimum, la solution est inchangée donc

Pour que la base demeure toujours optimale il faut et il suffit que

Conclusion: Dans le cas où xj serait une variable de base optimale et où la ième ressource n’est pas totalement utilisée, il est possible de modifier le coefficient aij d’une valeur δij égale à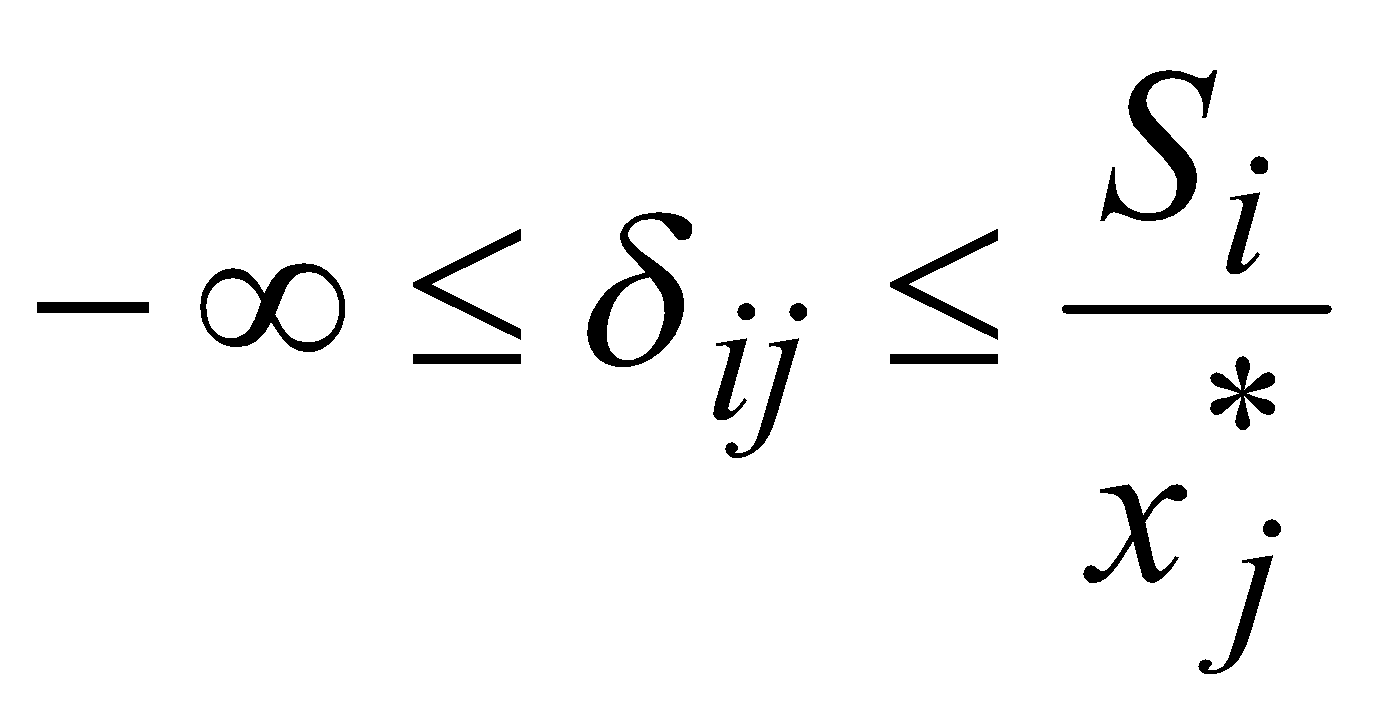

et la solution optimale demeure stable.

iii) Si xj est une variable hors base (xj = 0). Ceci implique qu’on ne va pas produire le produit j

Si δij ≥ 0, alors il est encore moins économique de fabriquer ce produit si le coefficient technologique aij augmenterait de δij

Si δij ≤ 0 , alors la fabrication du produit j peut devenir économique si on utilise moins de ressources.

V. Introduction d'une nouvelle activité

On sait déjà que la valeur optimale de la variables duale représentent les coûts marginaux (d’opportunité) associés à l’utilisation de ressources limitées.

On peut également utiliser ces coûts marginaux pour évaluer des décision concernant l’introduction de nouveaux produits ou de nouveaux procédés de fabrication.

a. Introduction d’une nouvelle variable de décision

L’agriculteur prévoit de produire des pommes de terre. Un hectare de pomme de terre demande 3 m3 d’eau et 2 heures de travail pour un revenu de C3 dinars.

La question est pour qu’elle valeur de C3, l’agriculteur a-t-il intérêt à introduire cette nouvelle production ?

Sans résoudre le nouveau programme linéaire suivant:

Max 100x1 + 200x2 + C3x3

S.c x1 + x2 + x3 ≤ 150

4x1 + 2x2 +3x3 ≤ 440

x1 + 4x2 + 2x3 ≤ 480

x1 ≤ 90

x1, x2, x3 ≥ 0

On peut déterminer si l’agriculteur a un intérêt à introduire la production ou pas.

En d’autres termes, s’il n’a pas intérêt à le faire, la solution optimale du programme linéaire ci-dessus donne x3 = 0. Ce qui revient à dire, que pour l’agriculteur l’utilisation d’un hectare de terrain, de 3 mètres cube d’eau et de deux heures de travail lui procurent plus de gain s’ils va les mettre au service de la production de tomates et/ou de piments plutôt que dans la production de pommes de terre. Ceci est équivalent au fait que la contrainte suivante:

n’est pas satisfaite (avec

sont les prix minimaux des ressources pour notre agriculteur).

Cette contrainte correspond à la 3ème contrainte du programme dual du programme linéaire ci-dessus :

On a :

, donc :

Si C3 < 200/3, l’agriculteur n’a pas intérêt à introduire la nouvelle activité
Si C3 > 200/3, l’agriculteur a intérêt à introduire cette nouvelle activité, la solution optimale va changer et la valeur de la fonction objectif augmentera
Si C3 = 200/3, l’agriculteur est indifférent envers l’introduction de cette nouvelle activité.

b. Introduction d’une nouvelle contrainte

Si la solution optimale satisfait la nouvelle contrainte, le problème admettra la même solution. Sinon l’introduction de cette contrainte va engendrer une nouvelle solution optimale.

➨ Chapitre 6 : Introduction à la Programmation Dynamique

Rechercher dans ce blog

Cours et Exercices

Dualité et analyse de sensibilité - Cours de La Recherche Opérationnelle