Introduction à la Programmation Dynamique - Cours de La Recherche Opérationnelle
COURS DE LA RECHERCHE OPÉRATIONNELLE
Cours Recherche Opérationnelle
Chapitre 1 : Formulation d’un programme linéaire (PL)I. Introduction
II. Les conditions de formulation d’un PL
III. Les étapes de formulation d’un PL
IV. Présentation Théorique
V. Exemples de formulations
Chapitre 2 : Résolution d’un programme linéaire (PL)
I. Introduction
II. Système d’axes
III. Représentation graphique des contraintes
IV. Représentation de la fonction objectif
V. Recherche de la solution optimale
a. Résolution graphique
b. Résolution par énumération :
VI. Exemples
VII. Analyse de sensibilité
Chapitre 3 :La Méthode de Simplexe
I. Introduction
II. Mise sous forme standard
III. Revue algébrique de la méthode du simplexe
IV. La méthode des tableaux
a. Tableau de simplexe initial
b. Amélioration de la solution
c. Calcul des tableaux suivants
V. Résumé de la procédure de la méthode du simplexe
VI. Exemple
Chapitre 4 : Problèmes de Minimisation et Problèmes Irréguliers
I. Introduction
II. Les variables artificielles
III. Les problèmes de minimisation
IV. Les problèmes irréguliers
a. Les problèmes impossibles
b. Les problèmes à solutions multiples
c. Les problèmes à solution infinie
d. Les problèmes à solution dégénérée
Chapitre 5 : Dualité et analyse de sensibilité
I. Introduction
II. Interprétation économique
III. Dualité
a. Définition
b. Propriétés et signification économique du programme dual
c. Tableau de correspondance primal-dual
III. Analyse de sensibilité
a. Analyse de sensibilité sur les Cj
b. Analyse de sensibilité sur les bj
c. Analyse de sensibilité sur les coefficients aij
IV. Introduction d’une nouvelle activité
a. Introduction d’une nouvelle variable de décision
b. Introduction d’une nouvelle contrainte
Chapitre 6 : Introduction à la Programmation Dynamique
I. Introduction
II. Exemple prototype. Le problème du voyageur
III. Caractéristiques d’un problème de programmation dynamique
IV. Programmation dynamique déterministe
a. Introduction
b. Problème du type plus court chemin
c. Répartition optimale des moyens
d. Résolution d'un programme linéaire
CHAPITRE 6
Introduction à la Programmation Dynamique
I. Introduction
La programmation dynamique est une technique mathématique qui a pour objet d’aider à prendre des décisions séquentielles indépendantes les unes des autres.
Contrairement
à la programmation linéaire, il n’y a pas un formalisme mathématique
standard. C’est une approche de résolution où les équations doivent être
spécifiées selon le problème à résoudre.
Notre exposé se base essentiellement sur de nombreux exemples qui illustrent cette technique.
II. Exemple prototype. Le problème du voyageur
Un
postier décide d’effectuer un voyage entre différentes villes qu’il ne
connaît pas. Son but est de choisir le chemin le moins dangereux. Pour
choisir son chemin, il s’informe auprès des assurances sur les
différentes valeurs des polices d’assurance de vie entre les différentes
routes possibles du voyage.
Le
trajet du postier est composé de 4 étapes (voir figure) et il doit
arriver à la ville numérotée 10 en partant de la ville numérotée 1. Les
autres numéros représentent les villes susceptibles d’être traversées.
Les arcs entre ces nœuds représentent les différents trajets possibles
et les valeurs cij au-dessus des arcs représentent le prix de la police d’assurance vie relatif au trajet décrit par l’arc.
Le chemin le moins dangereux est celui qui admet la plus petite valeur de la police d’assurance vie
Exemple : Si le voyageur empreinte le trajet 1→ 2→ 6→ 9→ 10 , le coût total de la police d’assurance est 13
Soit xn (n=1, ..., 4) les variables de décisions relatives à chacune des 4 étapes. Le chemin à suivre par le voyageur est 1→ x1→ x2→ x3→ x4 avec x4 = 10.
Soit fn (S, xn) le coût total de la police d’assurance vie pour le reste des étapes sachant que nous somme à l’état S de l’étape n et que la destination choisie est xn.
Etant donné S et n, soit  la valeur de xn qui minimise fn (S, xn) et soit
la valeur de xn qui minimise fn (S, xn) et soit  (S) la valeur minimale de fn (S, xn). (
(S) la valeur minimale de fn (S, xn). ( (S)= fn (S,
(S)= fn (S,  )).
)).
L’approche
de la programmation dynamique repose sur l’idée qu’un chemin ne peut
être optimal que si chacune des ses composantes est elle même optimale.
La démarche de la programmation dynamique consiste à étudier d’abord les
sous problèmes qui se situent chronologiquement les derniers et sur un
principe de retour en arrière.
L’objectif est donc de trouver la valeur de 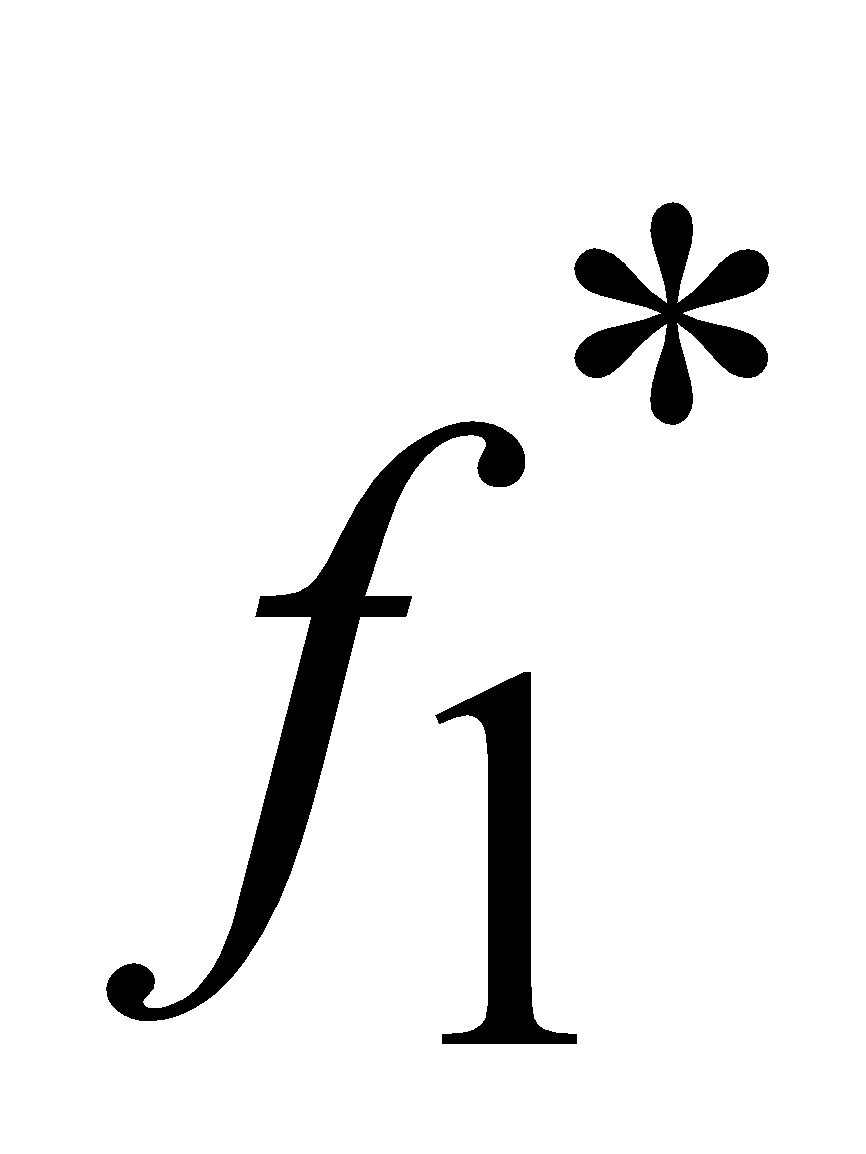 (1). Pour l’avoir, la programmation dynamique va essayer d’évaluer avec une procédure de chaînage en arrière
(1). Pour l’avoir, la programmation dynamique va essayer d’évaluer avec une procédure de chaînage en arrière  (s),
(s),  (s),
(s),  (s) et enfin
(s) et enfin  (1).
(1).
A chaque étape, on va essayer d’évaluer pour chaque état s, la valeur de f (S, xn) pour chaque destination xn possible, puis de retrouver la meilleure destination  (celle qui correspond au plus petit coût f(S, xn)) et aussi la valeur de
(celle qui correspond au plus petit coût f(S, xn)) et aussi la valeur de  (s).
(s).
Etape 4
x4
S
|
f4(S, x4))
| ||
8
|
3
|
3
|
10
|
9
|
4
|
4
|
10
|
Etape 3
f3(S, x3)=Csx3+
| ||||
x3
S
|
8
|
9
| ||
5
|
4(=1+3)
|
8(=4+4)
|
4
|
8
|
6
|
9
|
7
|
7
|
9
|
7
|
6
|
7
|
6
|
8
|
Etape 2
f2(S, x2)=Csx2+
| |||||
x2
S
|
5
|
6
|
7
| ||
2
|
11
|
11
|
12
|
11
|
5 ou 6
|
3
|
7
|
9
|
10
|
7
|
5
|
4
|
8
|
8
|
11
|
8
|
5 ou 6
|
Etape 1
f1(S, x1)=Csx1+
| |||||
x1
S
|
2
|
3
|
4
| ||
1
|
13
|
11
|
112
|
11
|
3 ou 4
|
La valeur de  (1) = 11
représente le coût total minimal de la police d’assurance vie. Le
chemin optimal n’est unique puisque dès le départ on peut choisir
(1) = 11
représente le coût total minimal de la police d’assurance vie. Le
chemin optimal n’est unique puisque dès le départ on peut choisir  = 3 ou 4, donc l’ensemble de ces chemins est:
= 3 ou 4, donc l’ensemble de ces chemins est:
1 →3 → 5 → 8 → 10
1 →4 → 5 → 8 → 10
1 →4 → 6 → 9 → 10
Exercice 1 : (Problèmes de transport)
Modéliser le problème de plus court chemin en utilisant la programmation linéaire ?
(Aide: Utiliser des variables du type binaires xi=0 ou 1)
III. Caractéristiques d'un problème de programmation dynamique
Nous
allons maintenant sur la base de l’exemple précédant analyser les
propriétés communes aux problèmes de programmation dynamique.
(i) Le problème peut être décomposé en étapes et une décision doit être prise à chaque étape.
Le
dernier exemple est devisé en 4 étapes où à chaque étape, la décision à
prendre est celle de la destination à choisir. Ces décisions sont
interdépendantes et séquentielles.
(ii)
A chaque étape correspond un certain nombre d’états. Dans l’exemple du
voyageur, les états à chaque étapes sont représentés par les villes que
le voyageur visité. Le nombre de ces états dans l’exemple est fini. Dans
ce qui suit en étudiera des problèmes où le nombre d’états est infinie (xn∈ IN) ou continue (xn∈ IR)
(iii)
A chaque étape, la décision prise transforme l’état actuel en un état
associé à l’étape suivante (dans certains cas avec une distribution de
probabilité).
Dans
notre exemple, se trouvant à une ville donnée, le voyageur décide de se
rendre à une autre ville qui est un état de l’étape suivante.
(iv)
Etant donné un état, une stratégie optimale pour les étapes restantes
est indépendante des décisions prises au étapes précédentes.
Si
le voyageur est dans un état quelconque de l’étape i, le chemin optimal
entre cet état et l’état 10 sera indépendant de la façon dont il y est
arrivé. En d’autres termes, l’état actuel contient toute l’information
nécessaire aux décisions futures. Cette propriété est dite principe
d’optimalité.
(v)
L’algorithme de recherche de la solution optimale commence par trouver
la stratégie optimale pour tous les états de la dernière étape.
(vi)
Une relation de récurrence identifie la stratégie optimale dans chaque
état de l’étape n à partir de la stratégie optimale dans chaque état de
l’étape n+1.
Dans notre exemple la relation est  (S)=
(S)=  {Csxn +
{Csxn + 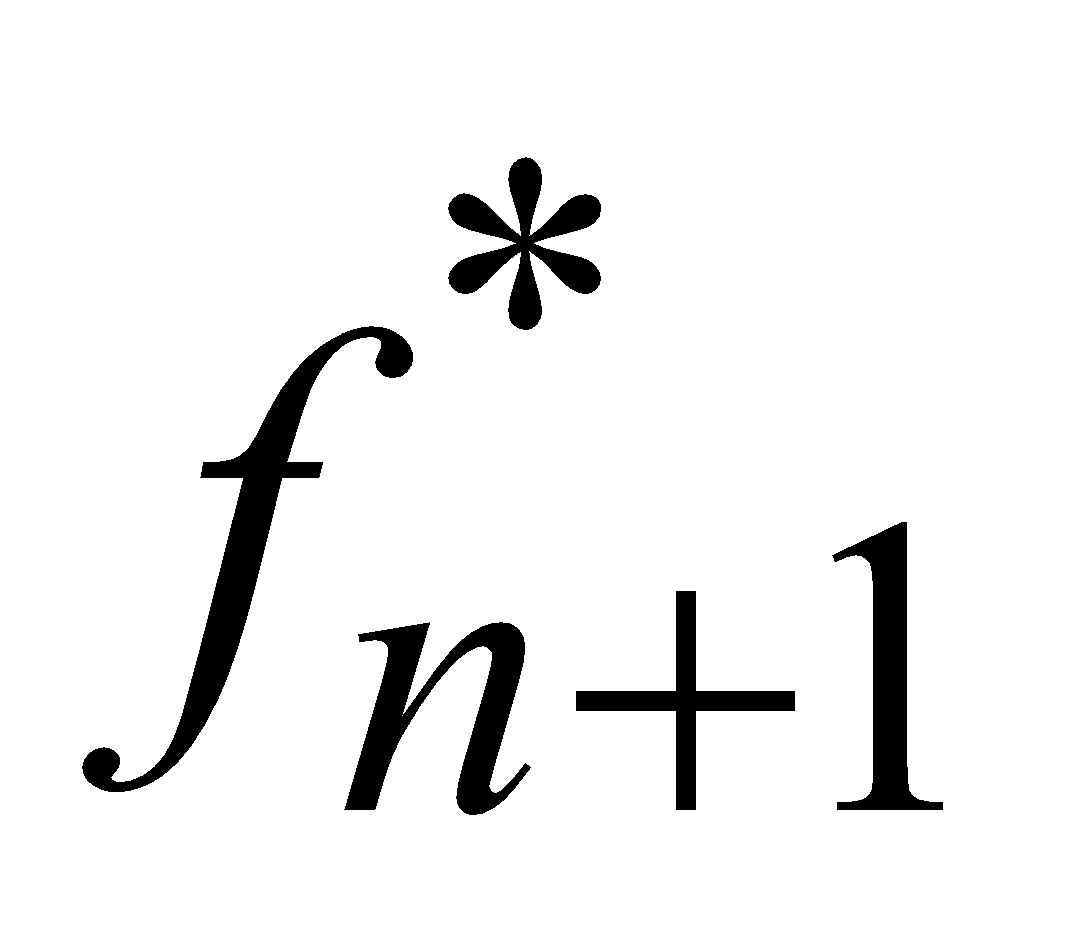 (xn)}
(xn)}
La stratégie optimale étant donné que nous sommes à l’état S de l’étape n, nécessite de retrouver la valeur de xn qui minimise l’expression ci-dessus.
La relation de récurrence à toujours cette forme 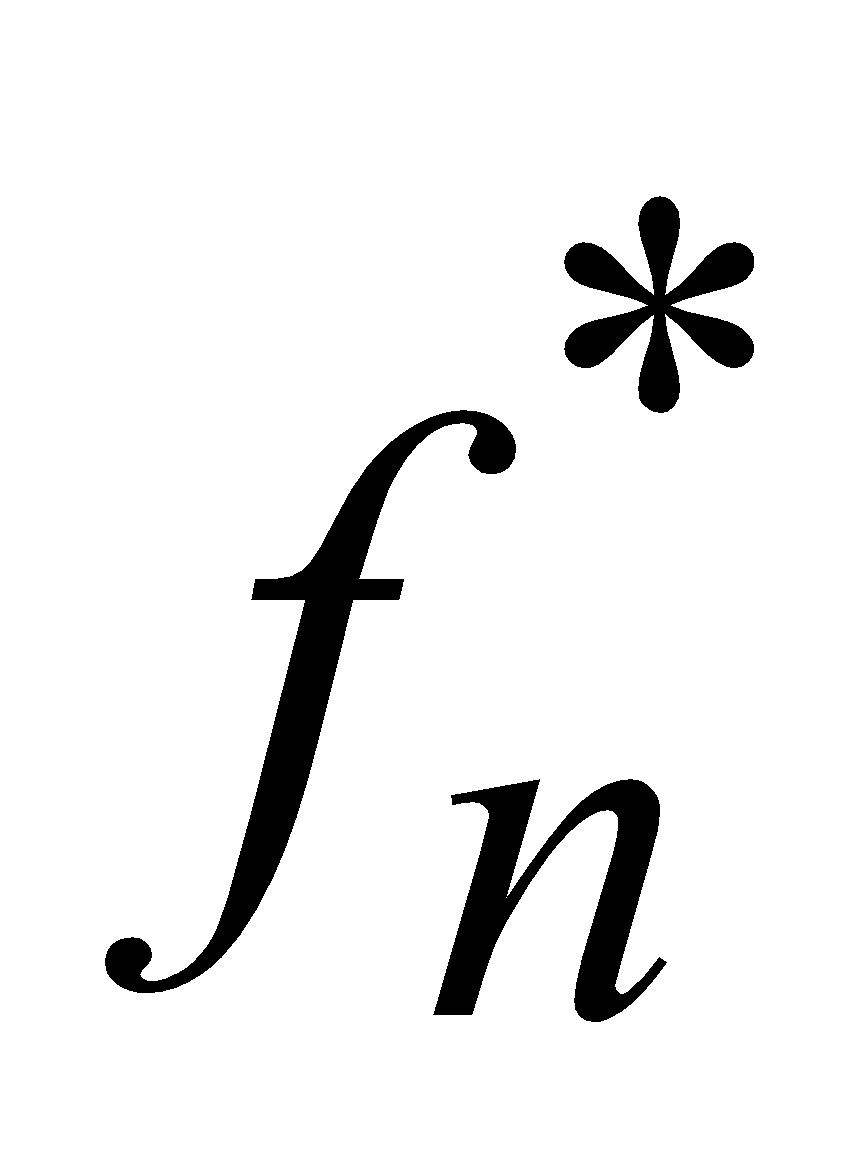 (S)=
(S)= 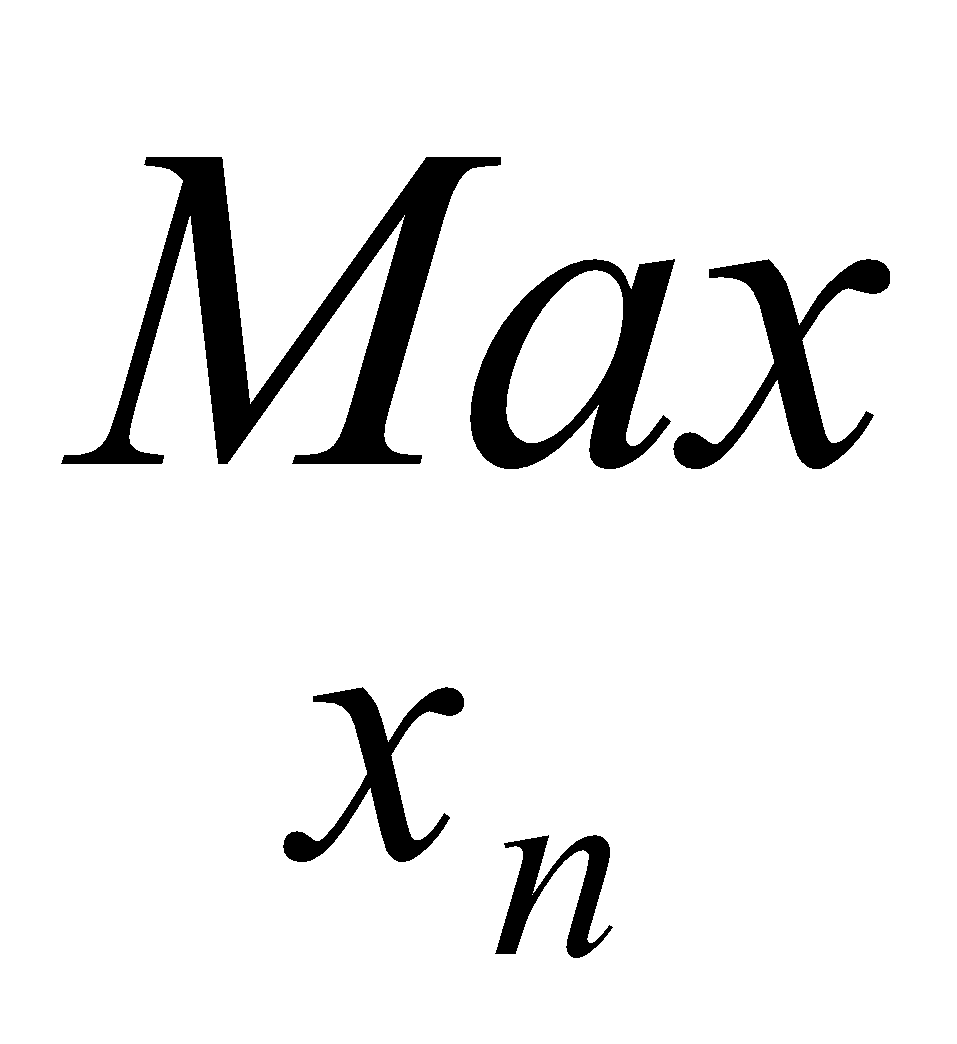 ou
ou  {fn(S,xn)},
{fn(S,xn)},
avec fn(S,xn) est une expression en fonction de S, xn et  (-)
(-)
(vii)
Utilisant cette relation de récurrence, l’algorithme procède à reculons
étape par étape. Il détermine la stratégie optimale pour chaque état de
chaque étape.
Dans tout problème de programmation dynamique, on peut construire à chaque étape un tableau analogue au suivant.
Etape n
fn(S, x1)
| |||
X1
S
|
états n+1
| ||
états n
|
le coût ou la distance
|
La longueur du chemin optimal à partir de S jusqu’à l’état final
|
Le meilleur état de l’étape n+1 le long du chemin optimal final
|
IV. Programmation dynamique déterministe
a. Introduction
Dans cette section on s’intéresse au problème dit déterministe, où la connaissance de l’état et de la décision à prendre suffisent pour savoir l’état à l’étape suivante.
Un
problème dynamique déterministe est caractérisé par la détermination de
la fonction objective. Cette fonction peut être le minimum de la somme
de la contribution induite par le passage d’un état à un autre, ou le
maximum d’une telle somme, ou le minimum du produit de ces termes… etc.
Il faut aussi déterminer la nature de l’ensemble des états dans chacune des étapes. Ces états Sn peuvent être représentés par des variables discrètes ou par des variables continues ou dans certains cas par un vecteur .
Quel est le plus court chemin de A à B ?
Solution:
On considère l'ensemble des états les point d'intersection sur les diagonales. Ainsi on a exactement 8 étapes.
fn(S, xn) = Csxn + fn+1 (xn), n=1,...., 8
avec f*n+1 (s) =  fn(S, xn) et f9 (S) = 0
fn(S, xn) et f9 (S) = 0
Etape 8
f8(S, B)
| |||
x8
S
|
B
| ||
1
|
3
|
3
|
B
|
2
|
2
|
2
|
B
|
Etape 7
f7(S, x7) = Csx7+ f8( x7)
| ||||
x7
S
|
1
|
2
| ||
1
|
7
|
-
|
7
|
1
|
2
|
5
|
6
|
5
|
1
|
3
|
-
|
6
|
6
|
2
|
Etape 6
f6(S, x6) = Csx6+ f7( x7)
| |||||
x6
S
|
1
|
2
|
3
| ||
1
|
12
|
-
|
-
|
12
|
1
|
2
|
9
|
8
|
-
|
8
|
2
|
3
|
-
|
7
|
11
|
7
|
2
|
4
|
-
|
-
|
7
|
7
|
3
|
Etape 5
f5(s, x5) = Csx5+
| ||||||
x5
S
|
1
|
2
|
3
|
4
| ||
1
|
16
|
-
|
-
|
-
|
16
|
1
|
2
|
16
|
11
|
-
|
-
|
11
|
2
|
3
|
-
|
12
|
8
|
-
|
8
|
3
|
4
|
-
|
-
|
10
|
11
|
10
|
3
|
5
|
-
|
-
|
-
|
15
|
15
|
4
|
Etape 4
f4(s, x4) = Csx4+
| ||||||||
x4
S
|
1
|
2
|
3
|
4
|
5
| |||
1
|
20
|
16
|
-
|
-
|
-
|
16
|
2
| |
2
|
-
|
14
|
10
|
-
|
-
|
10
|
3
| |
3
|
-
|
-
|
11
|
11
|
-
|
11
|
3,4
| |
4
|
-
|
-
|
-
|
16
|
20
|
16
|
4
| |
Etape 3
f3(s, x3) = Csx3+
| ||||||
x3
S
|
1
|
2
|
3
|
4
| ||
1
|
12
|
12
|
-
|
-
|
12
|
2
|
2
|
-
|
12
|
16
|
-
|
12
|
2
|
3
|
-
|
-
|
13
|
17
|
13
|
3
|
Etape 2
f2(s, x2) = Csx2+
| |||||
x2
S
|
1
|
2
|
3
| ||
1
|
15
|
15
|
-
|
15
|
1,2
|
2
|
2
|
16
|
14
|
14
|
3
|
Etape 1
f1(s, x1) = Csx1+
| ||||
x1
S
|
1
|
2
| ||
A
|
20
|
18
|
18
|
2
|
On peut résumer les résultats de la façon suivante:
Etapes
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Chemin optimal 1
|
A
|
2
|
3
|
3
|
3
|
3
|
2
|
1
|
B
|
Chemin optimal 2
|
A
|
2
|
3
|
3
|
4
|
3
|
2
|
1
|
B
|
La longueur du chemin optimal (1 ou 2) est égale à 18.
c. Répartition optimale des moyens
Un
projet du gouvernement est étudié par 3 groupes de chercheurs. La
probabilité que chacun de ces groupes 1, 2 et 3, n’arrive pas à terminer
le projet est respectivement: 0,4; 0,6 et 0,8.
Si on ajoute à ces groupes deux nouveaux chercheurs, les probabilités d’échec sont donné par ce tableau
Probabilité d’échec
| |||
Nbre de nouveaux chercheurs
|
Groupes
1 2 3
| ||
0
|
0,4
|
0,6
|
0,8
|
1
|
0,2
|
0,4
|
0,5
|
2
|
0,15
|
0,2
|
0,3
|
Le
problème est de déterminer l’allocation optimale de ces deux chercheurs
afin de minimiser la probabilité que les groupes de recherche échouent
dans leur travail.
Solution:
- Etapes: 3 étapes ou les états représentent le nombre de chercheurs disponibles
- Variable de décision: xn représente le nombre de chercheurs à allouer à l’équipe de recherche n, n = 1, 2, 3.
- Contribution de la décision xn est la probabilité que l’équipe n échoue après avoir eu xn chercheur de plus
(S) c’est la probabilité minimale que les groupes n,..., 3 échouent dans
leurs recherches :(S) =
fn(S, xn) n = 1, 2, 3
avec fn(S, xn) = pn(xn) ×(S, xn), pn(xn) est la contribution de la décision xn et
(s) =1.
Etape 3
f3(S, x3) = p3(x3)
| |||||
x3
S
|
0
|
1
|
2
| ||
0
|
0,8
|
-
|
-
|
0,8
|
0
|
1
|
0,8
|
0,5
|
-
|
0,5
|
1
|
2
|
0,8
|
0,5
|
0,3
|
0,3
|
2
|
Etape 2
f2(S, x2) = p2(x2)
| |||||
x2
S
|
0
|
1
|
2
| ||
0
|
0,48
|
-
|
-
|
0,48
|
0
|
1
|
0,3
|
0,32
|
-
|
0,3
|
0
|
2
|
0,18
|
0,2
|
0,16
|
0,16
|
2
|
Etape 1
f1(S, x1) = p1(x1)
| |||||
x1
S
|
0
|
1
|
2
| ||
2
|
0,064
|
0,06
|
0,072
|
0,06
|
1
|
La stratégie optimale est  = 1,
= 1, 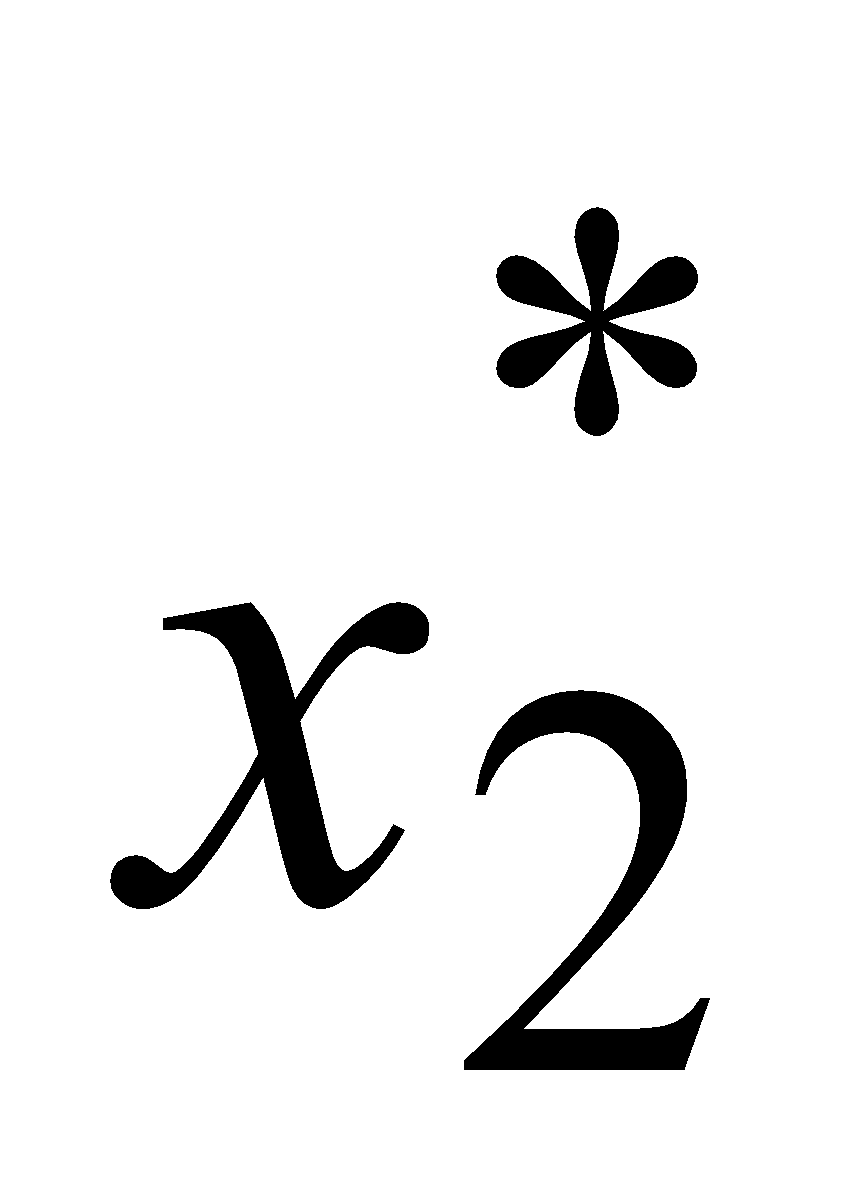 = 0 et
= 0 et 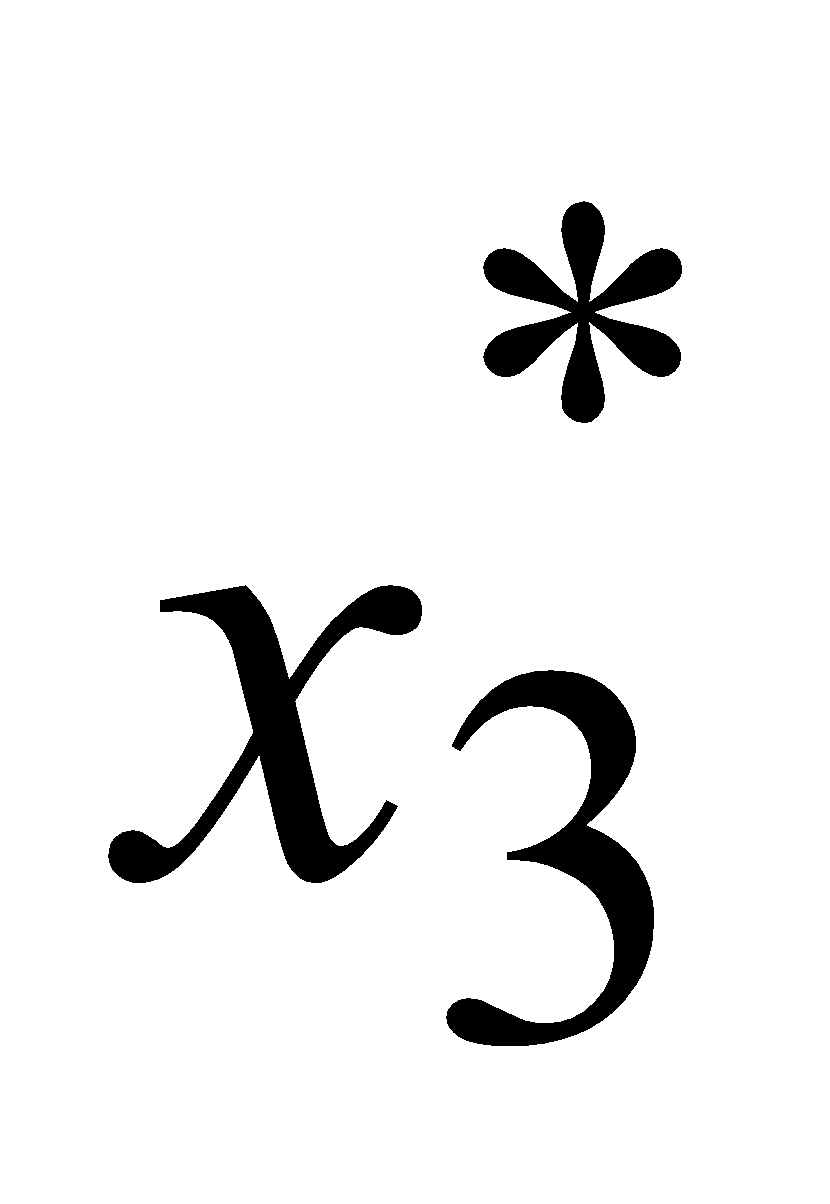 = 1.
= 1.
La probabilité d’échec des trois groupes de recherche est de 0,06.
Exercice 2 : (Problème de gestion des Stocks)
Un
magasin vend des chaussures de Ski. Par expérience, la période de vente
de ces chaussures dure 6 mois, du 1er Octobre jusqu’au 31 Mars.
Les prévisions de vente sont données par le tableau suivant:
Mois
|
Demande
|
Octobre
|
40
|
Novembre
|
20
|
Décembre
|
30
|
Janvier
|
40
|
Février
|
30
|
Mars
|
20
|
Le
magasin achète ces chaussures par lots de 10, 20, 30, 40 ou 50 paires
avec un coût de 4$ par paire et des réductions sur les prix d’achat.
Quantité
|
Solde
|
10
|
4%
|
20
|
5%
|
30
|
10%
|
40
|
20%
|
50
|
25%
|
Le
coût de lancement d’une commande d’approvisionnement est fixe, et est
de 2$. En plus un coût supplémentaire pour chaque ordre est de 8$ (coût
de transport des chaussures au magasin).
Le stock du magasin ne peut pas dépasser le nombre de 40 paires de chaussures par mois.
Une paire qui reste en stock à la fin du mois engendre un coût de 0,2$ par paire par mois.
Après
6 mois le magasin doit vendre toutes ces chaussures est le niveau des
stocks doit être nul. Sous l’hypothèse que la demande est fixe et
uniforme pendant chaque mois, retrouver la stratégie qui minimise le
coût total des stocks.
Solution:
Les étapes représente le début de chaque mois et les états le nombre de paires de chaussures en stock.
- Dn: demande à la nème étape
- xn: la commande au debut de la nème étape
- φ(xn) = 10 + Cn× xn avec Cn le coût d'achat.
- Pour n = 1,...,5,
(S)=
{φ(xn) +0,2(S+xn-Dn)+
(S+xn-Dn)} avec
(S)=0
Etape 6
A la dernière étape le stock restant est nulle donc les états possibles de cette étape sont 0, 10, 20.
S6
| ||
0
|
86
|
20
|
10
|
84
|
10
|
20
|
0
|
0
|
Etape 5
S6 = S5 + x5 – 30
f5(s, x5)= φ(x5) +0,2(S+x5-30)+  (S+x5-30)
(S+x5-30)
f5(s, x5)
| ||||||||||
S5
|
0
|
10
|
20
|
30
|
100
|
50
| ||||
0
|
-
|
-
|
-
|
204
|
188
|
164
|
164
|
50
| ||
10
|
-
|
-
|
172
|
168
|
142
|
-
|
142
|
40
| ||
20
|
-
|
134
|
136
|
122
|
-
|
-
|
122
|
30
| ||
30
|
86
|
98
|
90
|
-
|
-
|
-
|
86
|
0
| ||
40
|
50
|
52
|
-
|
-
|
-
|
-
|
50
|
0
| ||
Etape 4
S5 = S4 + x4 - 40
f4(s, x4)= φ(x4)+0,2(S+x5-30)+  (S+x5-30)
(S+x5-30)
f4(s, x4)
| ||||||||
S4
|
0
|
10
|
20
|
30
|
40
|
50
| ||
0
|
-
|
-
|
-
|
-
|
302
|
304
|
302
|
40
|
10
|
-
|
-
|
-
|
282
|
282
|
286
|
282
|
30,40
|
20
|
-
|
-
|
250
|
262
|
264
|
252
|
250
|
20
|
30
|
-
|
212
|
230
|
244
|
230
|
218
|
218
|
10
|
40
|
164
|
192
|
212
|
210
|
196
|
-
|
164
|
0
|
Etape 3
S4 = S3 + x3 - 30
f3(s, x3)= φ(x3)+2/3+1/3-30)
| ||||||||
S
|
0
|
10
|
20
|
30
|
40
|
50
| ||
0
|
-
|
-
|
-
|
420
|
422
|
414
|
414
|
50
|
10
|
-
|
-
|
388
|
402
|
392
|
384
|
384
|
50
|
20
|
-
|
350
|
370
|
372
|
362
|
323
|
323
|
50
|
30
|
302
|
332
|
340
|
342
|
310
|
-
|
302
|
0
|
40
|
284
|
302
|
310
|
290
|
-
|
-
|
284
|
0
|
Etape 2
S3 = S2 + x3 - 20
f2(s, x2)= φ(x2)+0,2+ (S2 + x2-20)
| ||||||||
S |
0
|
10
|
20
|
30
|
40
|
50
| ||
0
|
-
|
-
|
500
|
504
|
474
|
467
|
468
|
50
|
10
|
-
|
462
|
472
|
454
|
446
|
452
|
446
|
40
|
20
|
414
|
434
|
422
|
426
|
430
|
-
|
414
|
0
|
30
|
386
|
384
|
394
|
410
|
-
|
-
|
384
|
10
|
40
|
336
|
356
|
378
|
-
|
-
|
-
|
336
|
0
|
Etape 1
S2 = S1 + x1 – 40
f1(s, x1)= φ(x1)+0,2+ (S1 + x1-40)
| ||||||||
S
|
0
|
10
|
20
|
30
|
40
|
50
| ||
0
|
-
|
-
|
-
|
-
|
606
|
608
|
606
|
40
|
la politique optimale est 40, 50, 0, 40, 50, 0. Le coût est 606.
d. Résolution d'un programme linéaire
La
programmation linéaire peut être utiliser pour résoudre des programmes
linéaires de petite taille. On se limite ici à des programmes linéaires
du type entiers.
Considérons le programme linéaire suivant
Max 3x1 + 5x2
S.c 3 x1 + 2 x2 ≤ 9
4 x1 + 5 x2 ≤ 11
x1 ∈ IN , x2 ∈ IN
La décision à prendre est de déterminer les valeurs de x1 et x2.
On peut assimiler le problème à un programme dynamique à deux étapes,
où dans un premier temps, on doit déterminer la valeur de x1, et dans un deuxième temps la valeur de x2. Reste à savoir quels sont les états relatifs à chaque étape ?
Ces états doivent fournir l'information nécessaire pour aider à choisir notre décision.
Une
simple réflexion nous amène à considérer, le nombre de ressources non
utilisées dans les contraintes, comme étant des états possibles.
Un état est décrit par un vecteur (R1,R2), où R1 et R2 sont respectivement les ressources non utilisées dans la première et la deuxième contrainte.
A l'étape 1, l'unique état possible est S=(9,11).
La structure de base du problème est
étape n étape n+1
(R1,R2) (R1- a1n xn , R2- a2nxn )
cn xn
fn((R1,R2), xn) = cn xn +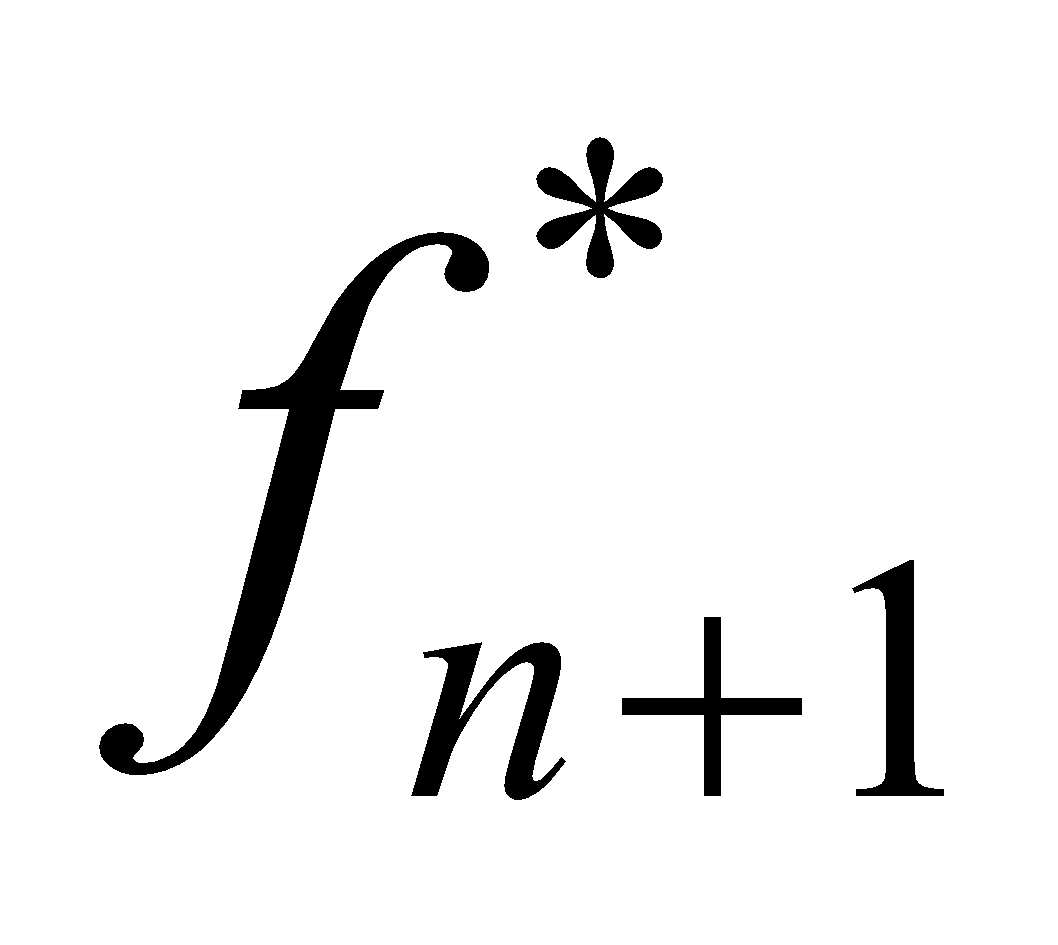 ((R1- a1n xn , R2- a2nxn ))
((R1- a1n xn , R2- a2nxn ))
avec  (R1,R2) =
(R1,R2) =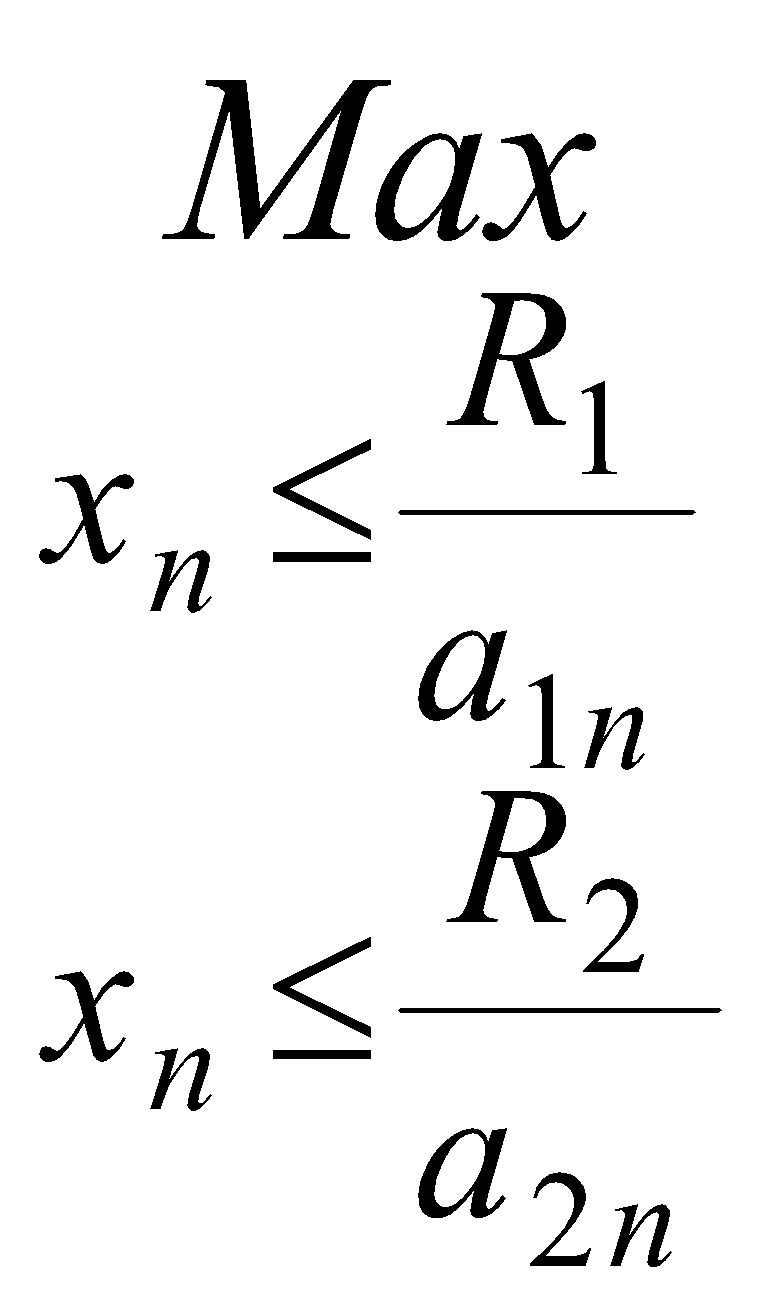 { fn((R1,R2), xn)} pour n=1,2 et
{ fn((R1,R2), xn)} pour n=1,2 et  (R1,R2)=0
(R1,R2)=0
Etape 2
A l'étape 2, si on considère toutes les combinaisons possibles des valeurs de R1 et R2
alors on aura à considérer un nombre d'état total égale à 99 états. Or
tous ces états ne sont pas réalisables dans le sens qu'on n'aura jamais
par exemple dans l'étape 2 l'état (10,8).
Ainsi, pour déterminer l'ensemble des états réalisables dans la
deuxième étape, il suffit de considérer toutes les valeurs possible de x1 (0,1 et 2), et avoir par conséquence les états suivant: (9,11), (6,7) et (3,3).
f2((R1,R2), x2) = 5 x2
| |||||
S |
0
|
1
|
2
| ||
9,11
|
0
|
5
|
10
|
10
|
2
|
6,7
|
0
|
5
|
-
|
5
|
1
|
3,3
|
0
|
-
|
-
|
0
|
0
|
Etape 1
On a : f1((R1,R2), x1) == 3 x1 +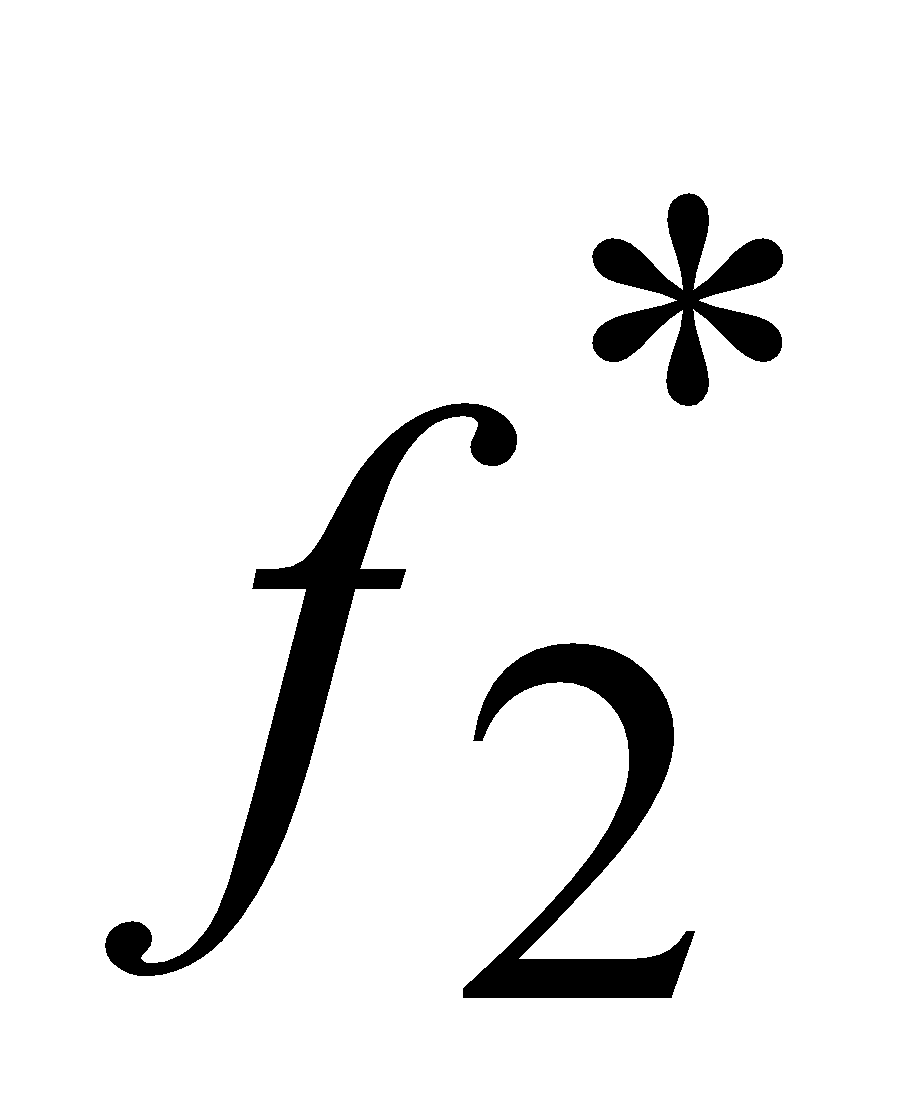 ((R1- 3 x1 , R2- 4 x1 ))
((R1- 3 x1 , R2- 4 x1 ))
f1((R1,R2), x1)
| |||||
S |
0
|
1
|
2
| ||
9,11
|
10
|
3+5=8
|
6
|
10
|
0
|
La solution optimale est (x1,x2)=(0,2) et la valeur de la fonction objectif est égale à 10.
Exercice 3: Résoudre les programmes linéaires suivants en utilisant la technique de la programmation dynamique:
- Max 4x1 + 5x2
S.c 8 x1 + 5 x2 ≤ 24
2 x1 + 5 x2 ≤ 13
x1 ∈ IN , x2 ∈ IN
La solution optimale est (x1,x2)=(1,2).
- Max x1 + 2 x2 + x3
S.c 3 x1 + 2 x2 ≤ 5
3 x2 + 2 x3 ≤ 7
x1 ∈ IN , x2 ∈ IN , x3 ∈ IN
La solution optimale est (x1,x2,x3)=(1,1,2).


Commentaires
Enregistrer un commentaire