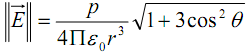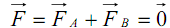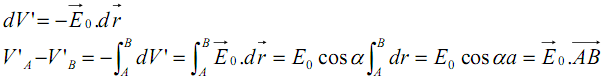Le Dipôle Électrostatique - Cours d’électrostatique

Le Dipôle Électrostatique

1 - INTRODUCTION

Un  dipôle électrostatique se définit par une répartition particulière de charges électriques telles que le barycentre des charges positives ne coïncide pas avec celui des charges négatives (le système est globalement neutre). Le dipôle le plus simple est donc un couple de deux charges de signe opposé distantes d'une longueur a non nulle. Cette notion est principalement utilisée en électromagnétisme et par suite en chimie où certaines liaisons entre molécules peuvent être expliquées en modélisant ces molécules par un dipôle (liaison hydrogène par exemple). En physique, on s'intéresse au champ électrostatiquecréé en un point r  éloigné du dipôle (on parle alors de dipôle actif). Mais on peut aussi étudier le comportement du dipôle lorsqu'il est placé dans un champ extérieur (on parle alors de dipôle passif).

2 - POTENTIEL ET CHAMP ELECTROSTATIQUES CREES PAR UN DIPOLE ISOLE 

2.1 - Définition

Le dipôle électrostatique est l’ensemble de  deux charges électriques  égales et de signes  contraires (-q) et (+q) (q > 0), (figure 1). Ces deux charges sont fixées respectivement en deux points A et B séparées d’une distance. On se propose d’étudier les caractéristiques  du champ et du potentiel électrostatique crées par ces deux charges en un point M très éloignés des charges :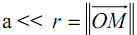: approximation dipolaire. 

2.2 - Moment dipolaires électriques 

Soient deux charges ponctuelles –q, +q fixées respectivement en A et B (q > 0). Le moment dipolaire électrique (ou moment du dipôle) est une grandeur vectorielle définie par (figure 1): 

En désignant par a la distance séparant A et B, la  norme du moment dipolaire vaut : 

Le moment dipolaire décrit la charge et sa géométrie. Il permet de caractériser le dipôle. Son unité dans le système International (SI) est le Coulomb-mètre (C m).

2.3 - Calcul du potentiel électrostatique 

Soient deux charges ponctuelles –q, +q fixées respectivement en A et B (figure 1) distant de (a). Considérons un point M très éloignés des charges, ce qui revient à considérer la distance a très inférieure à celle qui sépare M de l’une ou l’autre charge (la distance a est agrandie pour des raisons de clarté). 
La position de M est repéré dans le système des coordonnées polaires (r,  θ). Nous choisissons de prendre pour axe (Ox), la droite qui joint les deux charges tel que l’origine O soit au milieu du segment AB qui joint les charges (Ox es l’axe de révolution de la distribution). 
D’après le principe de superposition, le potentiel V(M) créé par le dipôle en un point M repéré par ses coordonnées polaires (r, θ) est donnée par :

avec, 

Ainsi, 

Nous avons donc,

Puisque  a/r<<1, on a :  a²/(4r²) <<a/r , on peut négliger les termes en (a/r)² devant le terme en (a/r) : 

Etant donné que a << r, on peut développeren puissance de (a/r) et ne retenir que le terme du premier ordre

Le potentiel V(M) est donc donné par : 

Soitle vecteur position du point M par rapport au point O (milieu de [A, B]) etle moment dipolaire (figure 2).  

On a :  

Le potentiel V(M) s’écrit donc : 

  Cette expression qui fait intervenir un produit scalaire est indépendante de tout système de coordonnées Il faut remarquer que la décroissance du potentiel en créer par un dipôle (1/r²) est plus rapide que dans le cas d’une charge ponctuelle qui est en (1/r).

2.4 - Calcul du champ électrostatique  

2.4.1 - Composantes du champ en coordonnées polaires

Le dipôle présente une symétrie de  révolution autour de (AB). Le champ électrostatique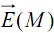est donc contenu dans le plan (M, AB) (figure 3).  

D’après le principe de superposition, le champ en M est donné par :

Pour calculer les composantes du champ, utilisons la relation : 

Les composantes du champ dérivant du potentiel V(M) s’écrivent dans le système de coordonnées cylindriques : 

Il faut remarquer que la décroissance du champ en (1/r^3) créés par un dipôle est plus rapide que dans le cas d’une charge ponctuelle qui est en (1/r²).

Le module de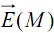est : 

Soit α l’angle que faitavec la radiale : 

  Notons que les composantes cartésiennes du champ suivant Ox  et Oy  (du plan AMB) s’écrivent :  

2.4.2 - Formulation globale du champ   

 Nous pouvons exprimeruniquement en fonction deet deen calculant le gradient de V(M) :

D’où l’expression intrinsèque deen fonction deet de: 

Les effets électriqueset V produits par le dipôle sont entièrement déterminés par son moment dipolaire. Il faut remarquer que la décroissance du potentiel en (1/r²) et du champ en (1/r^3) créés par un dipôle est plus rapide que dans le cas d’une charge ponctuelle.
  Notons que les composantes cartésiennes du champ suivant  Ox  et  Oy  (du plan AMB) peuvent être également obtenues en écrivant : 

  Ce qui donne d’après l’expression intrinsèque du champ indépendante du système de coordonnées : 

  On retrouve donc les composantes calculer à partir des composantes polaires du champ : 

3 - ACTION D’UN CHAMP EXTÉRIEUR UNIFORME SUR UN DIPÔLE

  Considérons un dipôle A(-q) et B( +q) de momentplacé dans un champ uniformeet tel que  ) ,(figure 4).  

3.1 - Forces et moment du couple exercés par un dipôle

Chacune des charges subit une force donnée par :

Puisque le champ extérieur est  uniforme, la résultante des forces est évidemment nulle (on ne tiendra pas compte de la force exercée par q sur –q et réciproquement) : 

Par contre, le dipôle subit un couple de forcedont le moment est : 

Ce qui donne : 

avec,  z u  est un vecteur unitaire de la direction (z’z) du repère (Oxyz). est un vecteur perpendiculaire au plan formé paret.
Si on libère le dipôle, il tend sous l’action deà tourner pour atteindre une position d’équilibre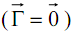dans laquelleetsont colinéaires :. 
•  Pour  α=0 (a le même sens que).  
Si on écarte légèrement le dipôle de sa position d’équilibre, le couple de force tend à le ramener à cette position (figure 5-a). L’équilibre est stable. 
•  Pour  α=Π (est antiparallèle à).
Si on écarte légèrement le dipôle de sa position d’équilibre, le couple de force tend à l’éloigner de cette position (figure 5-b). L’équilibre est instable.

  Ainsi, l’action mécanique principale d’un champ uniforme est qu’il tend à orienter le dipôle suivant les lignes du champ. 

3.2 - Energie potentielle d’interaction du dipôle 

C’est l’énergie nécessaire pour amener +q et –q de l’infini à leur position en B et A.
Les charges –q et +q fixées en A et B ont des énergies potentielles égales àet. Ainsi, l’énergie potentielle d’interaction W associé au champ extérieurest : 

Soit V’ le potentiel dont dérive le champ. 

Ainsi,  

Cette expression représente l’énergie d’interaction du dipôle associée au champet n’a rien à voir avec  l’énergie de interne du dipôle (énergie nécessaire pour amener une charge de l’infini à une distance a de l’autre). Nous retrouvons les positions d’équilibre :
•  Pour  0 = α  (a le même sens que),
L’énergie potentielle est minimale et l’équilibre est stable.
•  Pour  Π = α  (est antiparallèle à),
L’énergie potentielle est maximale et l’équilibre instable.  

4 - Conclusion

Le champ créé par un dipôle dans le  cadre de l’approximation dipolaire est proportionnel à 1/r^3 et le potentiel à 1/r² , alors que pour une charge ponctuelle, le champ créé est proportionnel à 1/r² et le potentiel à 1/r.

∎ Retour aux plan de cours d’électrostatique