Nappe chargée uniformément en surface - La solution d'exercice - Exercices corrigés d'életrostatique
a) Variable dont dépend 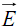 et sa direction
et sa direction
La nappe chargée en surface est contenue dans le plan (xOy) comme le montre la figure 1.
* La plan chargé est invariant par translations suivant Ox et Oy. Le système des coordonnées le plus adapté au calcul de
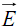 est le système cartésien de base
est le système cartésien de base  . Le champ
. Le champ 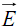 est indépendant de x et y :
est indépendant de x et y :
* Le plan passant par M et perpendiculaire à (Ox) est un psp (plan de symétrie pair.
passant par M et perpendiculaire à (Ox) est un psp (plan de symétrie pair. 
* Le plan passant par M et perpendiculaire à (Oy) est un psp (plan de symétrie
passant par M et perpendiculaire à (Oy) est un psp (plan de symétrie
 passant par M et perpendiculaire à (Ox) est un psp (plan de symétrie pair.
passant par M et perpendiculaire à (Ox) est un psp (plan de symétrie pair. 
* Le plan
 passant par M et perpendiculaire à (Oy) est un psp (plan de symétrie
passant par M et perpendiculaire à (Oy) est un psp (plan de symétrie
De plus, le plan chargé xOy étant un plan de symétrie paire, le champ 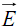 en un point M’ symétrique de M par rapport à ce plan est :
en un point M’ symétrique de M par rapport à ce plan est :
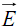 en un point M’ symétrique de M par rapport à ce plan est :
en un point M’ symétrique de M par rapport à ce plan est :
b) Calcul du champ électrostatique 
Tenant compte de la symétrie de la distribution plane de charge, nous choisissons comme surface fermée Σ le parallélépipède droit, dont les génératrices sont normales au plan chargé, fermé par deux sections droites notées Σ1 et Σ2 d’aire S, passant respectivement par M(x, y, z) et par M’(x, y, -z) le symétrique de M par rapport au plan xOy (figure 2).
Le flux
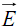 sortant de la surface latérale Σ1 du cylindre est nul, car en tout point de Σ1,
sortant de la surface latérale Σ1 du cylindre est nul, car en tout point de Σ1, Le flux sortant de Σ se réduit au flux sortant de Σ1 et Σ2 :
La charge à l’intérieure de la surface de Gauss est :
D’après le théorème de Gauss :
Ces deux résultats peuvent être condensés sous la forme :
Ce résultat peut être retrouvé en choisissant comme surface de Gauss Σ la surface fermée formé par le cylindre droit, dont les génératrices sont normales au plan chargé, fermé par deux sections droites d’aire S, passant par M(x, y, z) et par M’(x, y, -z).
Le champ
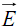 change de sens à la traversée de la nappe chargée et subit une discontinuité égale à 0 / σ/ε0 (figure 3).
change de sens à la traversée de la nappe chargée et subit une discontinuité égale à 0 / σ/ε0 (figure 3). En réalité, il n’existe pas de distribution plane de dimensions infinies. Cependant, la distribution plane est considérée comme infinie si on ne considère que des points placés loin des bords de la distribution, c’est à dire des points dont la distance à la surface chargée est petite par rapport aux dimensions de celle-ci.
c) Calcul du potentiel électrostatique V(M)
En choisissant l’origine des potentiels dans le plan xOy : V(z=0)=0
A la traversée du plan chargé, le potentiel y est continu (figure 4).
.


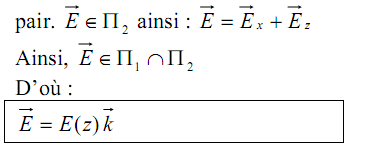











Commentaires
Enregistrer un commentaire