Sphère chargée uniformément en volume - La solution d'exercice - Exercices corrigés d'életrostatique

a) Variable dont dépend et sa direction

Les mêmes considérations de symétrie évoquées précédemment suggèrent que : 

b) Calcul du champ électrostatique

Pour une sphère fermé Σ de centre O et de rayon r, le flux sortant est : 

Puisque le norme du champ est constant, le théorème de Gauss s’écrit : 

* M est extérieur à (S) : r ≥ R
  La charge volumique à l’intérieur d’une sphère de rayon r ≥ R est donnée par :  

Le théorème de Gauss donne : 

 En simplifiant par (4 Π), on a : 

 Le champ électrostatique est porté par et on a : 

 * M est intérieur à (S) : r ≤ R
   La charge volumique à l’intérieur d’une sphère de rayon r ≥ R est donnée par :  

Le théorème de Gauss donne : 

 En simplifiant par (4 Π r² ), on a : 

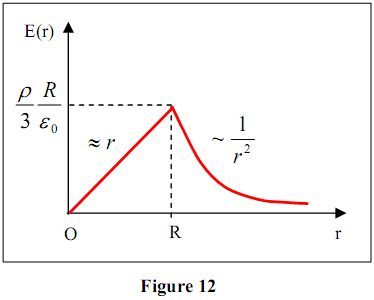
 Le champ électrostatique est porté par et on a : 

  Remarquons que pour r ≥ R, le champ est le même que si la charge concentrée au centre de la sphère O (figure 12).

c) Calcul du potentiel électrostatique V(M) 

Pour déterminer la constante nous pouvons utiliser la continuité du potentiel pour r = R : 

Ainsi pour   r ≥R , le champ et le potentiel sont les mêmes que si toute la charge Q était concentrée en O (figure 13). 

 Remarque
Le potentiel pour un point M à l’intérieur à  Σ peut être également déterminé en écrivant : 

∎ Retour Aux Exercices