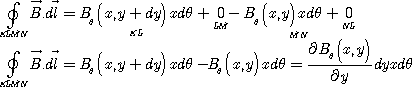La solution d'Exercice sur Champ magnétique à l’intérieur d’un tore (Théorème d'Ampère. Flux du champ magnétique)





1. Caractéristiques de la distribution et du champ magnétique.
Le plan contenant le point M et l’axe Oy est un plan de symétrie de la distribution de courants : le champ magnétique en ce point y est perpendiculaire.
D’autre part la distribution est invariante par rotation autour de l’axe Oy.
Ces deux propriétés permettent d’exprimer le vecteur champ magnétique sous la forme :
avecle vecteur unitaire orthoradial de la base cylindro-polaire.

Les lignes de champ de sont des cercles de centre situés sur l’axe Oy contenus dans des plans perpendiculaires à cet axe.

2. Norme du champ magnétique.
Pour déterminer la norme de ce champ magnétique on utilise le théorème d’Ampère en prenant comme contour d’Ampère une ligne de champ passant par le point M(x, y) considéré :

 Comme le contour choisi est contenu dans un plan y = cste, la composante du champ est constante, on obtient :






Ce résultat est vrai quelque soit le contour d’Ampère choisi dans un plan y = cste, on peut donc en déduire que ce champ ne dépend pas de la coordonnée d’espace y.
On peut montrer cela en utilisant un contour d’Ampère élémentaire KLMN compris entre y et y + dy comme l’illustre le schéma suivant :
 On applique à nouveau le théorème d’Ampère sur ce contour :

Comme le contour considéré n’enlace aucun courant la circulation du champ est nulle, on obtient alors :
 On constate ainsi que le champ magnétique ne dépend pas de y. Ainsi :

3. Flux du champ magnétique.
Le fluxdu champ magnétique est défini par :

4. Détermination du rapport a/R.
Champ maximal :

Champ minimal :
 On obtient :

Le rapport demandé est donc égal à :







Cours Et Exercices