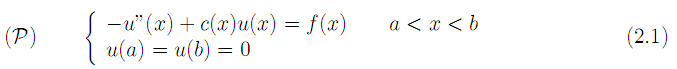Formulation variationnelle
1. Exemple 1-D
C² ([a,b]) telle que u(a) = u(b) = 0 et ∀x ∈]a,b[, −u”(x)+c(x)u(x) = f (x).
En faisant le produit scalaire L²(]a,b[) de l’´équation différentielle avec une fonction-test v∈D(]a,b[) (c’est a` dire en intégrant sur [a,b]), on a :
car v(a) = v(b) = 0 puisque v ∈ D(]a,b[). Chaque terme de cette ´équation a en fait un sens d`es lors que v∈H1(]a,b[). De plus, D(]a,b[) étant dense dans H1(]a,b[) (cf §1.4.3) ,cette équation est vérifiée pour tout v ∈ H1(]a,b[).
On peut donc définir le nouveau problème :
Ce problème est la formulation variationnelle (ou formulation faible) du problème (P). Toute solution de (Q) est appelée solution faible. Il est immédiat que toute solution forte de (P) est aussi une solution faible.
Une solution classique de ce problème est une fonction de C2(Ω¯ ) vérifiant (2.3) en tout point de Ω. Au passage, on voit que ceci impose que f soit C0(Ω¯ ). Toute solution classique vérifie
soit par intégration par parties :
Les exemples précédents montre que, d’une fac¸on générale, la formulation variationnelle sera obtenue en faisant le produit scalaire L²(Ω) de l’´équation avec une fonction v appartenant à un espace V à préciser (c’est à dire en multipliant par v et en intégrant sur Ω), et en intégrant par parties les termes d’ordre les plus élevés en tenant compte des conditions aux limites du problème. On arrive alors a` une formulation du type :
ou` a(.,.) est une forme sur V × V (bilinéaire si l’EDP de départ est linéaire) et l(.) est une forme sur V (´linéaire si les conditions aux limites de l’EDP de départ le sont).
Soit `a résoudre le problème
ou` f et c sont des fonctions données continues sur [a,b]. On supposera de plus que la fonction
c est strictement positive sur [a,b]. Un tel problème
est appel´e problème aux limites.
Définition: Une solution classique (ou solution forte) de
(P)
est une
fonction de
.
En faisant le produit scalaire L²(]a,b[) de l’´équation différentielle avec une fonction-test v∈D(]a,b[) (c’est a` dire en intégrant sur [a,b]), on a :
soit, en intégrant par parties le premier terme :
car v(a) = v(b) = 0 puisque v ∈ D(]a,b[). Chaque terme de cette ´équation a en fait un sens d`es lors que v∈H1(]a,b[). De plus, D(]a,b[) étant dense dans H1(]a,b[) (cf §1.4.3) ,cette équation est vérifiée pour tout v ∈ H1(]a,b[).
On peut donc définir le nouveau problème :
Ce problème est la formulation variationnelle (ou formulation faible) du problème (P). Toute solution de (Q) est appelée solution faible. Il est immédiat que toute solution forte de (P) est aussi une solution faible.
2. Exemple 2-D
Soit Ω ouvert borné de IRn. On veut résoudre le problème
Une solution classique de ce problème est une fonction de C2(Ω¯ ) vérifiant (2.3) en tout point de Ω. Au passage, on voit que ceci impose que f soit C0(Ω¯ ). Toute solution classique vérifie
donc :
soit par intégration par parties :
On peut donc définir le nouveau problème :
C’est la formulation variationnelle de (P). On voit aussi que ce problème est défini d`es lors que f∈L2(Ω).
3. Formulation générale
Les exemples précédents montre que, d’une fac¸on générale, la formulation variationnelle sera obtenue en faisant le produit scalaire L²(Ω) de l’´équation avec une fonction v appartenant à un espace V à préciser (c’est à dire en multipliant par v et en intégrant sur Ω), et en intégrant par parties les termes d’ordre les plus élevés en tenant compte des conditions aux limites du problème. On arrive alors a` une formulation du type :
Trouver u
∈ V
tel
que a(u,v) = l(v) ∀v
∈ V (2.5)
ou` a(.,.) est une forme sur V × V (bilinéaire si l’EDP de départ est linéaire) et l(.) est une forme sur V (´linéaire si les conditions aux limites de l’EDP de départ le sont).
Remarque : Une formulation plus générale est la suivante :
Trouver u
∈ V
tel
que a(u,w) = l(w) ∀w∈W (2.6)
ou` a(.,.) est une forme bilinéaire sur V × W et l(.) est une
forme linéaire sur W . V est alors appel´e espace des solutions et W
espace des fonctions-tests. La formulation précédente (2.5) correspond
donc au cas particulier W = V