La solution d'exercice ondes et vibrations :Un roulement à billes
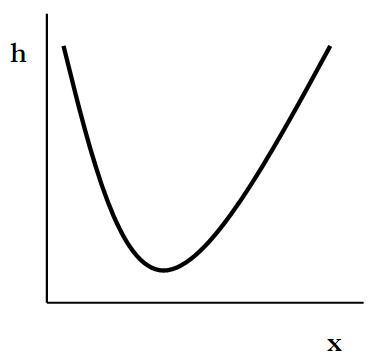
1)Comme x → 0, h → + ∞, et comme x → + ∞, h → + ∞. Aussi il ya une seule valeur de x pour laquelle
est égal à zéro, à savoir :
(De la première observation, ou en regardant la dérivée seconde de h, il devrait être clair que h(x0) est un minimum local.) Ces deux faits signifient h(x) doit ressembler à :
Vous pourriez également avoir déduit justement de la première déclaration sur les limites de h (x) et la forme des fonctions √x et x.
2)Un point d'équilibre est celle à laquelle la force nette agissant sur un objet est égal à zéro. Depuis
ceci est équivalent à l'affirmation selon laquelle un point d'équilibre est celui où la dérivée spatiale de la fonction d'énergie potentielle est nulle. Pour que notre système, l'énergie potentielle est tout simplement l'énergie potentielle gravitationnelle U(x) = mgh(x). Par conséquent, à partir de (1), il n'y a qu'un point d'équilibre.3) De dessus, il y a un seul point d'équilibre,
La balle roule en avant et en arrière autour de ce point. Comment pouvons-nous déterminer la fréquence d'oscillation? Il y a trois raisons de penser que l'expansion en série de Taylor pourrait nous aider:
-toute oscillation est harmonique
-nous considérons "des petites oscillations" en l'équilibre, ce qui amène pour une série de Taylor.
-Plus important encore: Notre balle est oscillant dans un paysage de l'énergie "familier" potentiel
Et si nous développons. En général, l'expansion de U (x) = x environ x0 est :
L'application de cela à notre U (x) développé au sujet de notre point d'équilibre, nous notons que le (x-x0) terme est nul, puisque la dérivée de U est nul là-bas, et ainsi de
Pour les petites oscillations, on peut négliger les termes d'ordre supérieur. Donc, cela ressemble à Uressort= (1/2) kx2, car il est seulement une constante fois un déplacement quadratique! Vous pourriez être inquiet qu'il y est un terme constant U(x0) dans l'expression ci-dessus qui ne se présente pas dans Uressort, mais cela n'a pas d'importance - on peut ajouter ou soustraire arbitrairement une constante de toute fonction d'énergie potentielle; depuis F=-dU/dx, ces constantes ne se traduisent pas en une force physique significative. Vous pourriez être inquiet que Uressort= (1/2) kx2, tandis que notre expression implique (x-x0)² . Mais pensez à ce que cela signifient ces symboles - au ressort, x est le déplacement de l'équilibre, tandis que pour notre boule, (x-x0) est le déplacement de l'équilibre. D'où notre (x-x0) et x la carte du ressort sur le même concept physique.
Par conséquent, notre bal "ressemble à" un-ressort-de-masse , avec une constante de raideur efficace