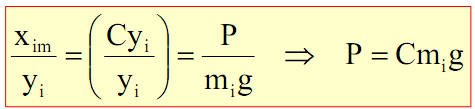Critères de Conception d’Arbres - Elements de machines

Qu'est-ce qu'un arbre ?

‰ rotative ou fixe, normalement de section circulaire qui supporte des éléments de transmission de puissance ou de mouvement (engrenages, poulies, etc.) qui porte les noms suivants :
- arbre de transmission (shaft) qui transmet un couple d’un moteur
- arbre de renvoi qui supporte des éléments de machines et transmet un couple entre les éléments : poulies, etc.
- essieu - arbre stationnaire (axle) ou rotatif qui ne transmet pas de couple et donc sert au positionnement

Conception d’arbres

 Fonction : transmettre de la puissance longtemps et à bon coût. Par conséquent, les critères de choix du matériau sont les suivants :

1. Propriétés mécaniques
2. Coût
3. Usinabilité
4. Disponibilité
5. Résistance à la corrosion
6. Autres

Démarche de conception basée sur la résistance

1. Calculer les réactions
2. Calculer la répartition des couples de torsion
3. Calculer la répartition des moments de flexion dans les plans vertical (Mv) et horizontal (Mh)
4. Calculer la répartition du moment de flexion résultant (M)
5. Calculer la répartition des forces axiales

En se basant sur une des  théories de limitations, déterminer le diamètre de l’arbre dans la section critique permettant de résister aux charges imposées ou vérifier la sécurité à la section critique (si le diamètre est connu).

Conception basée sur la résistance

Trois approches présentées :
1. Approche du code ASME.
Méthode simple, utile en conception pour évaluation rapide du diamètre de l’arbre. Basée sur le critère de Tresca (les contraintes sont statiques).
2. Théorie du cisaillement maximal (code Westinghouse).
Basée sur le critère de Tresca et la ligne de Soderberg en fatigue.
Prend en charge les valeurs moyenne et alternée des contraintes.
3. Théorie de von Mises-Hencky (méthode VMHG).
Basée sur le critère de von Mises et la ligne de Goodman en fatigue.
Prend en charge les valeurs moyenne et alternée des contraintes.

Code ASME (charges statiques)

 
 FS est inclus dans le calcul des contraintes permises

Code ASME (facteurs de charge)

Note: le facteur de sécurité est implicitement inclus dans le calcul de Sp

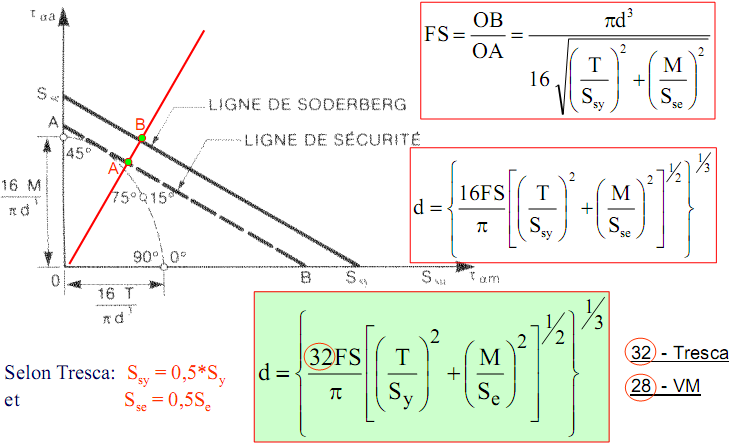
Code Westinghouse (charges variables)

I. Charges sur l’arbre :

II. Écoulement selon critère de Tresca :

III. Ligne de Soderberg pour des charges statiques et alternées : 

Code Westinghouse (charges cycliques)

Variations des composantes de contraintes de cisaillement tracées sur le diagramme de Goodman

Code Westinghouse (cas général)

Ta et Ma - composantes variables
Tm et Mm - composantes statiques (moyennes)

Méthode Von Mises-Hencky-Goodman (VMHG)

Un arbre en rotation est soumis à :
‰ - des contraintes de flexion variables causées par un moment constant
‰ - des contraintes de cisaillement variables causées par un couple variable
‰ - des contraintes axiales causées par une charge axiale constante

Procédure pour la méthode VMHG

1. Identifier les sollicitations sur l’arbre et calculer la valeur approximative de d (code ASME, par exemple).
2. Calculer les composantes statiques et variables des contraintesrésultantes.
3. Calculer les contraintes de Von Mises σm’et σa’.
4. Appliquer l’équation de conception de Goodman.
5. Calculer le FS (vérification) ou d (conception).
6. Répéter les calculs (1 à 5) en cas de besoin.

Construction d’un DCL

Diagramme de Goodman modifié

Équations générales pour la méthode VMHG

Équations simplifiées pour la méthode VMHG

T est le couple de torsion constant
M est le moment de flexion constant

Conception basée sur la rigidité

La variation des flèches de part et d’autre d’un engrenage doit être inférieure à 0.005/F (F est la largeur de la dent en pouce)

Critère de déformation

La rigidité d’un arbre dépend :
‰ - du diamètre (d)
‰ - du module de Young (E) du matériau
             Les arbres sont généralement fait d’acier 
             Tous les aciers ont à peu près le même E
             Donc le diamètre de l’arbre détermine la rigidité

Déformation latérale permise (flèche maximale en fonction de la portée entre les supports) :
‰-  pour les arbres de transmission : 0.08 %
‰-  pour les arbres de renvoi : 0.015 %

Calcul de la déformation latérale

Méthode des moments d’aire est basée sur deux théorèmes :
1. La différence de pente entre deux points A et B sur une poutre est égale à la surface au-dessous du diagramme M/EI entre les points A et B.
2. La flèche tangentielle mesurée verticalement entre un point A sur la poutre et la tangente au point B est égale au premier moment de surface sous le diagramme M/EI par rapport à A.

Méthode des moments d’aire

Méthode des moments d’aire est basée sur deux théorèmes :
1. La différence de pente entre deux points A et B sur une poutre est égale à la surface au-dessous du diagramme M/EI entre les points A et B.

 2. La flèche tangentielle mesurée verticalement entre un point
A sur la poutre et la tangente au point B (∆AB) est égale au premier moment de surface sous le diagramme M/EI par rapport à A.

 Déformation en torsion

Déformation en torsion permise
• pour les arbres de transmission :  angle de torsion doit être inférieur à 1° sur une distance de vingt fois le diamètre de l’arbre.
• pour les arbres de renvoi : angle de torsion doit être inférieur à 0.3° par  mètre de longueur (charge constante) et à 0.15° par mètre de longueur (charge subite).  

T - couple de torsion, L - longueur de l’arbre, G - module de cisaillement, J - module d’inertie polaire

Conception basée sur la vitesse 

Conception basée sur la vitesse de rotation critique

La fréquence de résonance est liée à la rigidité Or, la rigidité d’un arbre dépend :
• du diamètre (d)
• du module de Young (E) du matériau

‰-  Les arbres sont généralement fait d’acier
- ‰ Tous les aciers ont à peu près le même E
‰ - Donc le diamètre de l’arbre détermine la fréquence de résonance

Vibration d’arbres

Principe de conservation d’énergie : dans un système conservatif (amortissement nul) vibrant à une fréquence
naturelle, toutes les masses ont un mouvement harmonique simple et à la même fréquence. On peut  donc écrire :

Aspects énergétiques

Hypothèse de Rayleigh

La forme de l’élastique de l’arbre en vibration est semblable à l’élastique de l’arbre soumis à un chargement statique provenant de la répartition des masses sur l’arbre.

yi est la flèche au point «i» correspondant à l’ensemble des charges mig

Fréquences de vibration de l’arbre (Rayleigh)

Énergies cinétique et potentielle maximales

Vitesse critique déterminée selon Rayleigh

Comme la déformation statique est  plus faible que la déformation dynamique réelle, l’hypothèse de  Rayleigh a pour  conséquence de rigidifier l’arbre.

Si K augmente (la rigidité est plus élevée), ω augmente aussi.
Par conséquent la méthode de Rayleigh donne une évaluation supérieure de la vitesse critique.

Approximation de Dunkerley 

Dunkerley propose une autre approximation de la vitesse critique :

 Les ωi sont calculées comme si une seule charge existait à la fois.
ω1 : vitesse critique si seule la masse 1 existe.
ω2 : …


Équation de Dunkerley

Cette approche donne une évaluation  inférieure de la vitesse critique.

Manuels de références :

• Shigley, Mischke and Budynas, «Mechanical Engineering Design», 7e éd., McGraw Hill, 2004, Chapter 18.
• Drouin, Gou, Thiry et Vinet «Éléments de machines» Éditions de l'École Polytechnique, 1982-86, chapitre 6.
• Hamrock, Jacobson and Schmid «Fundamentals of Machine Elements» McGraw Hill, 1999, Chapter