Cylindre chargé uniformément en surface - La solution d'exercice - Exercices corrigés d'életrostatique

a) Variable dont dépend 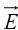et sa direction

* Le cylindre chargé a un axe de révolution Oz (figure 5). Le système de coordonnées le plus adapté est le système cylindrique de base . Cette distribution de charge est invariante par translation suivant Oz et par rotation d’angle θ autour de Oz.  

* Le plan   passant par M et l’axe (Oz) est un psp (plan de symétrie pair.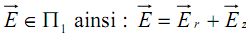 

* Le plan passant par M et perpendiculaire à (Oz) est un psp (plan de symétrie pair. 
 

 D’où, le champ est radial : 

 

Le système possède une symétrie de  révolution par rapport à l’axe  z z'  et de translation parallèlement à cet axe : le champ  E  en un point M situé à la distance r de l’axe  est donc de la forme : 

b) Calcul du champ électrostatique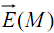  

La surface fermée Σ que nous choisissons pour calculer le flux de 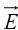est une surface de même type que la surface chargée constitué d’un cylindre d’axe  z z' , de rayon r, de hauteur h (figure 6).  

Le flux de 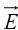à travers la surface de Gauss s’écrit : 

Le flux de à travers les surfaces planes Σ₁ et Σ₂ étant nul (en tout point de ces surfaces, on a  ). Le flux sortant de Σ se réduit à : 

 avec, Σ₁ : surface latérale de Σ
  Puisque E(r) et r sont des constantes, on a :

Le théorème de Gauss s’écrit : 

* Si M est extérieur au cylindre chargé (C) : r > R
La charge à l’intérieur du cylindre Σ de rayon r > R : 

 Puisque σ est uniforme, on a : 

Le théorème de Gauss s’écrit donc : 

 En simplifiant par (2 Π h), la norme du champ électrostatique E(r) : 

Par raison de symétrie, on sait que est porté par . On obtient finalement : 

* Si M est intérieur au cylindre chargé (C) : r < R
Dans ce cas, la charge à l’intérieur du cylindre Σ de rayon r < R étant nulle, 
Q_int =0
Il s’ensuit, d’après le théorème de Gauss, que la norme du champ est nulle : 
 E(r)=0 
Ce qui conduit à :

 Le champ 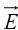normal à la surface chargée, subit une  discontinuité égale à σ₀ /ε₀ (figure 7). 

c) Calcul du potentiel électrostatique V(M) 

* Si M est à l’extérieur du cylindre : r ≥ R 

Dans le cas d’une distribution  surfacique portée par  le cylindre infiniment long, on prendra l’origine des potentiels, à une distance finie r₀ de l’axe du cylindre (par exemple  r₀ > R ; V(r₀) = 0) 

* Si M est à l’intérieur du cylindre : r ≤ R  
  V ( r≤)= cste 
La constante est déterminée par continuité du potentiel en r=R : 

∎ Retour Aux Exercices