Sphère chargée uniformément en surface - La solution d'exercice - Exercices corrigés d'életrostatique
a) Variable dont dépend et sa direction
et sa direction
* La sphère chargée est invariante par double rotation l’une d’angle θ autour de
 et l’autre d’angle ϕ autour de
et l’autre d’angle ϕ autour de : on dit que la sphère a le point O comme centre de symétrie (figure 8). Le système de coordonnées le plus adapté est le système sphériques de base
: on dit que la sphère a le point O comme centre de symétrie (figure 8). Le système de coordonnées le plus adapté est le système sphériques de base  .
.* Le plan méridien
 est un psp (plan de symétrie pair.
est un psp (plan de symétrie pair.  ainsi :
ainsi :* Le plan
 passant par M etperpendiculaire à (Oz) est un psp (plan desymétrie pair.
passant par M etperpendiculaire à (Oz) est un psp (plan desymétrie pair. 
D’où, le champ est radial :
Le champ
 créé par cette distribution à symétrie sphérique, en un point M est porté par le vecteur
créé par cette distribution à symétrie sphérique, en un point M est porté par le vecteur  et ne dépend que de la variable d’espace r= ||OM|| .
et ne dépend que de la variable d’espace r= ||OM|| .
 b) Calcul du champ électrostatique
b) Calcul du champ électrostatique
La surface fermée Σ que nous choisissons pour calculer le flux de
 est une sphère de centre O, de rayon r : surface de même type que la surface chargée (figure 9). Le flux de
est une sphère de centre O, de rayon r : surface de même type que la surface chargée (figure 9). Le flux de à travers Σ est donné par :
à travers Σ est donné par :La charge à l’intérieur de la surface de Gauss Σ dépend de la position de M. Deux cas peuvent être distingués : M est extérieur à la sphère chargé (S) ou M est intérieur à (S).
* M est extérieur à (S) : r > R
La charge à l’intérieur de la sphère Σ de rayon r > R est :
Le théorème de Gauss s’écrit donc :
En simplifiant par (4 Π), la norme du champ s’écrit :
Par raison de symétrie, le champ
 est porté par
est porté par  . On obtient finalement :
. On obtient finalement :
Le champ est identique au champ créé en M par une charge ponctuelle égale à la charge totale de la sphère, Q concentrée en O.
* M est intérieur à (S) : r < R
Dans ce cas, la charge à l’intérieur de la sphère de rayon r < R est nulle :
Le champ électrostatique E(r) subit à la traversée de la surface chargée une discontinuité égale à σ/ε0 (figure 10).
c) Calcul du potentiel électrostatique V(M)
* M est extérieur à (S) : r ≥ RLe potentiel en M est :
En choisissant l’origine des potentiels à l’infini V=(r=∞)=0, on obtient :
Le potentiel est identique au potentiel créé en M par une charge ponctuelle égale à la charge totale de la sphère, Q.
* M est intérieur à (S) : r ≤ R
Le champ en tout point intérieur à S est nul ; le potentiel est donc constant :
Pour déterminer la constante nous pouvons utiliser la continuité du potentiel pour r = R :
Nous pouvons retrouver cette constante en écrivant :
avec, V(r=0) est le potentiel au centre O de la sphère S obtenu à partir d’un calcul direct suivant la relation :
Alors que le champ est discontinu à la traversée de la charge (figure 10), le potentiel électrostatique est continu (figure 11).







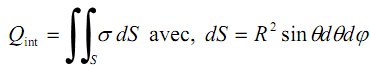














Commentaires
Enregistrer un commentaire