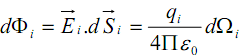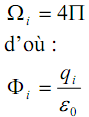Théorème De Gauss - Cours d’électrostatique
Théorème De Gauss
1 - INTRODUCTION
Dans le calcul de la circulation du champ électrostatique
, nous avons utilisé le fait queest de la forme
et nous avons en déduit la relation entre le champ E et le potentiel V. Nous allons maintenant déduire une équation du champqui dépend spécifiquement du fait que f(r) est en 1/r². Les développements qui suivent s’appliquent donc aux champ de la forme
. 2 - FLUX DU CHAMP ELECTROSTATIQUE
2-1 - Cas d’une charge ponctuelle
a) Flux élémentaire
Soit une charge ponctuelle q>0 placée en O et M un point de l’espace (figure 1).
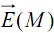créé par q en M est : 
à travers la surface orientée est : 
b) Flux sortant à travers une surface fermée
Soit une surface fermée Σ. On se propose de calculer le flux du champ électrostatiquecréé par une charge ponctuelle q à travers la surface fermée Σ. Plus précisément on s’intéresse au flux sortant, donc on a choisi d’orienter le vecteur
dans le sens de la normale sortante à Σ. Deux cas seront envisagés : • le cas où la charge q est située à l’extérieure de la surface Σ
• et celui où la charge q est située à l’intérieur de la surface Σ
Nous désignons par l’indice i les charges situées à l’intérieur de Σ et par l’indice e les charges extérieures à Σ. Soit
le champ créé par qi et
le champ créé par qe. 1èr Cas : La charge est située à l’extérieur de Σ
Nous pouvons calculer le flux sortant de la surface fermée Σ (figure 2) à partir des flux élémentaires. En effet, traçons un cône élémentaire de sommet O (où se trouve la charge extérieur à Σ, qe) et d’angle solide |dΩ| . Ce cône découpe sur la surface Σ deux surfaces élémentaires dS1 en M1 et dS1’ et M1’. Soient
les vecteurs sortant des surfaces dS1 et dS1’. L’angle solide sous lequel du point O on voit les surfaces élémentaires orientées dS1 et dS1’, a la même valeur absolue, mais de signes opposés à cause de l’orientation du vecteur normalpar rapport à
(figure 2) :
les vecteurs sortant des surfaces dS1 et dS1’. L’angle solide sous lequel du point O on voit les surfaces élémentaires orientées dS1 et dS1’, a la même valeur absolue, mais de signes opposés à cause de l’orientation du vecteur normalpar rapport à(figure 2) : 
Si on considère le flux du champ
créé par la charge qe située en O, sortant des surfaces dS1 et dS1’, d’après (1) et (2), on obtient : 
sortant de la surface Σ,
, on peut balayer toute la surface Σ à l’aide de cônes élémentaires tels que celui de la figure 2. Chacun de ces cônes intercepte sur la surface Σ une paire de surfaces élémentaires dS1 et dS1’ telles que leur contribution au flux total,
. On en conclut que le flux du champ électrostatique crée par une charge ponctuelle située à l’extérieur d’une surface fermée Σ, sortant de la surface Σ est nul :
2ème Cas : La charge est située à l’intérieur de Σ
Soit (C) le cône élémentaire de sommet O et d’angle solide dΩ1 (figure 3).
au flux total, non nulle. Le flux élémentaire dΦi crée par
à travers une surface élémentaire dSi (figure 4) est donnée par : 
est l’angle solide sous lequel du point O, on voit la surface fermée Σ ; Ωi est donc l’angle solide sous lequel du point O on voit tout l’espace : 
2-2 - Cas de n charges ponctuelles
Considérons ni charges à l’intérieure d’une surface fermée (Σ) et ne charges situées à l’extérieure de cette surface. Le champcréé par les n charges
est la somme vectorielle des champs créées par chacune des charges : 
sortant de la surface Σ est : 
Ce résultat constitue le théorème de Gauss.
2-3 - Cas d’une distribution continue de charge
On peut écrire le théorème de Gauss dans le cas où la distribution de charges est continue et décrite par une densité volumique de charges ρ. La charge totale intérieure à Σ, c’est à dire contenue dans le volume v limité par la surface fermée Σ est :
Dans ce cas le théorème de Gauss s’écrit, v étant le volume limité par la surface (Σ) :
2-4 - Validité du théorème de Gauss
Précisons que ce théorème est obtenu à partir de la loi de Coulomb (loi fondamentale de l’électrostatique). Ce théorème reste valable quand les charges sont en mouvement.Le théorème de Gauss est une conséquence :
1) de la loi en 1/r² régissant les interactions entre les charges électriques
2) du caractère central des forces électrostatiques
3) du principe de superposition
Nous présentons dans le tableau ci-dessous la formulation du théorème de Gauss pour le champ électrostatique.
Cependant, ce théorème est également valable pour tous les champs de vecteurs de la forme
, en particulier pour le champ de gravitation
. 3 - SYMETRIE ET INVARIANCE DE LA DISTRIBUTION DE CHARGE ET CARACTERISATION DU CHAMP ET DU POTENTIEL
On rappelle que le calcul du champ électrostatique E , crée par une distribution de charge de densité volumique ρ peut être mené, soit à partir :• de la loi de Coulomb :
• du théorème de Gauss sous sa forme intégrale:
est la normale à la surface fermée englobant la charge q. 3-1- Symétries des sources ( causes) et des effets crées : Principe de Curie
Les effets présentent les mêmes symétries que leurs causes. Les éléments de symétrie des causes (distributions D ou sources) doivent donc se retrouver dans les effets (et V) produits. a) Distribution de charge présentant un plan de symétrie pair (Π)
On dit qu’une distribution de charge (D) est symétrique par rapport à un plan Π, si pour deux points P et P’ symétriques par rapport à Π, on a (figure 5) :
. 
Pour illustrer ce cas, nous prenons deux charges identiques q placées en P et P’, où P’ est le symétrique de M par rapport au plan Π.
Soit M’ le symétrique du point M par rapport au plan Π. On peut constater sur la figure 6 que le champ en M’ est le symétrique du champ en M :
On remarque que les composantes du champ parallèles au plan de symétrie
sont conservées alors que celles perpendiculaires au plan
sont inversées : 
Le champ électrique est contenu dans le plan de symétrie paire. Dune façon générale tout vecteur polaire est contenu dans le plan de symétrie paire (figure 7).
b) Distribution de charge présentant un plan de symétrie impair (Π’)
Une distribution de charge possède un plan de symétrie impaire Π’, si pour deux points P et P’ symétriques par rapport à Π’, on a
Soit M’ un point symétrique de M par rapport à Π’, On peut constater sur la figure 8 que le champ en M’ est l’opposé du symétrique du champ en M :
c) Conséquences
Lors d’une opération de symétrie appliquée à la distribution de charges (D), le champ électrostatiquesubit la même opération. On dit que le vecteur champ électrique est un vecteur polaire ou “vrai” vecteur. Ce vecteur a les mêmes propriétés de symétrie que ses sources. Les plans de symétrie nous permettent souvent de trouver la direction du champ en un point M. Pour trouver la direction du champ
en un point M, il suffit de trouver : * Soit deux plans de symétrie passant par M. Le champ
appartenant à ces deux plans. Il est donc porté par la droite formée par leur intersection. * Soit un plan de symétrie impair passant par M. La direction du champ
au point M est donnée par la normale au plan de symétrie impaire. Les plans de symétrie permettent d’obtenir les composantes du champ
. 3-2 - Invariance de la distribution de charge
a) Invariance par translation le long d’un axe
Les variables dont dépendent ces composantes sont obtenues en étudiant les invariances de la distribution de charges.Dans la plupart des cas nous utilisons des distributions idéalisées, par exemple pour calculer le champ
crée par un fil en un point M de l’espace homogène et isotrope, très proche du fil, on peut considérer que le fil est infini. Considérons l’exemple d’un fil rectiligne caractérisé par une densité linéique λ uniforme. Si on translate le fil parallèlement à lui même d’un vecteur
, la nouvelle distribution D’ coïncide avec D (puisque le fil est considéré infini et la distribution de charge est uniforme). (figure 10-a). 
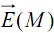et le potentiel V(M) sont inchangés en un point M quelconque de l’espace homogène et isotrope : 
, il vient : 
(annexe 1), les relations précédentes deet V s’écrivent 
b) Invariance par rotation autour d’un axe
Considérons une répartition de charge D de densité volumique uniforme ρ présentant un axe de révolution, c’est à dire si on fait subir à cette distribution une rotation d’angle θ autour de cet axe, la nouvelle distribution D’ coïncide avec la précédente (la distribution reste invariante) (figure 11-a).
. Si on considère un point M’ quelconque obtenu par rotation du point M d’un angle θ on aura (figure11-b) :
et V (ici a deux ρ et z). 4 - CONCLUSION
Le théorème de Gauss établit une relation entre le flux du champ électrique à travers une surface fermée et la charge à l'intérieur de cette surface. Cette relation a les propriétés suivantes :- elle reflète les propriétés générales des champs électriques et ne se limite pas aux champs électrostatiques (contrairement à la loi de Coulomb);
- elle permet de déterminer plus simplement l’expression du champ électrostatique créé par les distributions de charges qui présentent une symétrie appropriée (sphérique, cylindrique, plan, etc.).